四平方の定理(図形の面積と正射影)
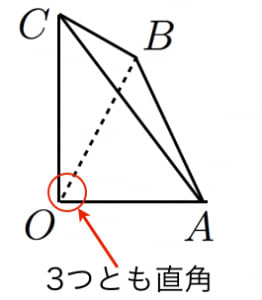
4つの面のうち3つが直角三角形である図のような三角錐(直角三角錐,三直角四面体)において,
ただし, で三角形 の面積を表します。三平方の定理の三次元空間バージョンです! デカルト・グアの定理,あるいはド・グアの定理とも呼ばれます。
四平方の定理の証明
四平方の定理の証明
一般化
一般化
実は,直角三角錐だけでなく,もっと一般の図形でも四平方の定理は成立します!
面積が であるような三次元空間内の平面図形を 平面に正射影した図形の面積を とおく。同様に も定義する。このとき
平面への正射影とは,もとの図形に 軸方向から光を当てたときの影です。
が三角形のとき,さきほどの四平方の定理と一致するので,この定理はさきほどの定理の一般化になっています。
正射影と面積
正射影と面積
上記の定理を証明するためには前提知識が二つ必要になります。
「平面 に含まれ,面積が である図形」を平面 に正射影したときの面積は である。ただし, は平面 と平面 のなす角。

これは有名な性質なので覚えておきましょう。 が(一辺が平面 と の交線と平行な)長方形の場合には簡単に確認できます。一般の図形はそのような長方形がたくさん集まったものとみなすことで納得できます(厳密には積分)。
平面 と平面 のなす角は,それぞれの平面の法線ベクトルがなす角に等しい。
これは実際に平面(紙など)を二つ使って納得してください!
一般バージョンの証明
一般バージョンの証明
の長さ の法線ベクトルを とおく。
平面の法線ベクトルは なので,二つの法線ベクトルがなす角のコサインは(内積を考えることで) となる。
よって, と 平面のなす角を とおくと,前提知識2より
となる。
さらに,前提知識1より なので,
同様に であるので,
を得る。
ちなみに,四平方の定理というと整数論におけるラグランジュの四平方和定理(→整数論の美しい定理7つの5つ目)のことを指す場合もあるので注意して下さい。
地味ですがかなりおもしろい定理だと思います。











