ボロノイ図とその3つの性質
点(母点)がいくつか与えられたとき,どの点に一番近いかによって平面を分割したものをボロノイ図(Voronoi diagram)と言う。
ボロノイ図について,意味と性質をわかりやすく説明します。特に3つめの性質がおもしろいです。
ボロノイ図の例
ボロノイ図の例
図は母点の数が 個であるボロノイ図の例です(フリーハンドで書いたので誤差はご勘弁ください)。辺は垂直二等分線の一部,交差点は外心になります。
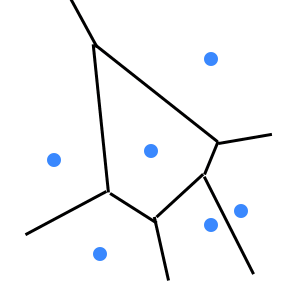
ボロノイ図は「各母点の勢力範囲を表す」と解釈できます。実際にいろいろな問題に応用されています。
今回は平面+通常の距離(ユークリッド距離)の場合のみを考えますが,別の空間や距離でボロノイ図を考えることもできます。
ボロノイ図は凸
ボロノイ図は凸
ボロノイ図の各領域は凸である。
ここで,領域 が凸とは,二点 なら線分 が に含まれることを言います。へこんでいないという意味です。
母点 のボロノイ領域に属する二点 を取ってくる。
また,他の母点の一つを とする。
「 よりも に近い点の集合」は半平面をなす(境界は の垂直二等分線)。この半平面に が属しているので,線分 全体もこの半平面に属す。
つまり,線分 上の任意の点は「 よりも に近い」を満たす。以上の議論は各 について成立するので,線分 は のボロノイ領域に含まれる。
ボロノイ図の空円性
ボロノイ図の空円性
以下,ボロノイ図の辺をボロノイ辺,頂点をボロノイ点と言います。
ボロノイ点には三本以上のボロノイ辺が接続しています(もし二本しか接続していないと隣接するボロノイ領域のいずれかが凸でなくなる)。
ボロノイ点を中心とし,その点に隣接する領域(三つ以上ある)の母点を通る円は,(内部に)他の母点を含まない。
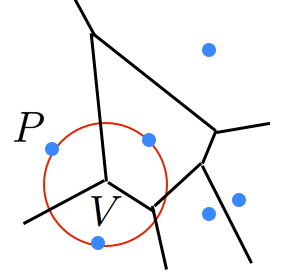
背理法で証明する。ボロノイ点を ,その点に隣接する領域の母点の一つを とする。 を中心とし を半径とする円の中に別の母点 が含まれるとすると, となる。
よって, のすぐ近くの点は よりも が近くなるため, に隣接する領域の母点の一つが であることに矛盾。
ボロノイ点,ボロノイ辺の数
ボロノイ点,ボロノイ辺の数
少し難しいですが,一番おもしろいです!
母点の数を ,ボロノイ点の数を ,ボロノイ辺の数を とすると,
ボロノイ図の点や辺の数は母点の数の数倍でおさえられる,つまりボロノイ図はそんなに複雑にならないということですね。証明には平面グラフにおけるオイラーの多面体定理を用います。
ボロノイ図を十分大きな円でカットした平面グラフ を考える。 の頂点数を ,枝数を ,面の数を とおくと,オイラーの多面体定理から である。
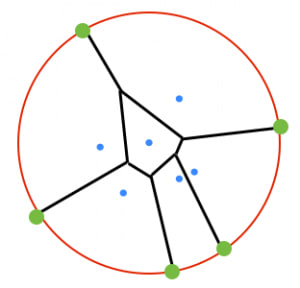
円周上の点の個数を とすると, , である。また,一番外側の領域も面数 にカウントされているので である。
以上より, ,つまり
また,各ボロノイ点には三本以上の枝が接続しているので,
ただし,ボロノイ辺は一つまたは二つのボロノイ点に接続する(無限遠に伸びるものは一つの点のみと接続)ことを使った。
以上二つの式から を消去すると
を消去すると, を得る。
性質3の証明は,データ構造とアルゴリズム(杉原厚吉著)という本を参考にしました。
性質3の証明で が消えるとこが素晴らしいですね!











