ベクトルの定番問題を一瞬で解く公式
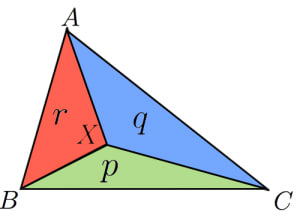
三角形 内に点 があり,
が成立するとき,面積比は
頻出なので,この結果をそのまま覚えておくとよいでしょう。
公式の導出
公式の導出
より,始点を に変換すると,
変形すると となる。
は線分 を に内分する点なので,
が分かる。対称性より残りも同様。
特に のときは,点 は三角形 の重心と一致します。
確認の例題
確認の例題
公式の証明での式変形が身についているか,次の問題でチェックしましょう。
三角形 の内部に点 があり, が成立するとき,次の問いに答えよ。
-
を と で表せ。
-
2直線 と の交点を とする。 および を求めよ。
面積比は自分でチェックしてください!
-
与式より であるため,変形すると となる。
-
1番より となる。 は 上にあるため となる。よって となる。
→高校数学の問題集 ~最短で得点力を上げるために~のT103では,類題と,この問題で計算ミスをしないためのコツを紹介しています。
3次元への拡張
3次元への拡張
同様の議論を四面体に適用すると,以下の公式を得ます:
四面体 内に点 があり,
が成立するとき,四面体の体積比は
内分の公式は比率を反対にしてしまいがちなので注意しましょう。
Tag:三角形の面積を求める公式まとめ











