単位ベクトルの求め方といろいろな具体例
単位ベクトルの意味・求め方・関連する話題を紹介します。
単位ベクトルの意味
単位ベクトルの意味
単位ベクトルとは,長さ(大きさ)が1のベクトルのことです。
-
というベクトルは長さが1なので単位ベクトルです。

-
というベクトルは長さが1なので単位ベクトルです。実際,長さは三平方の定理より になります。

-
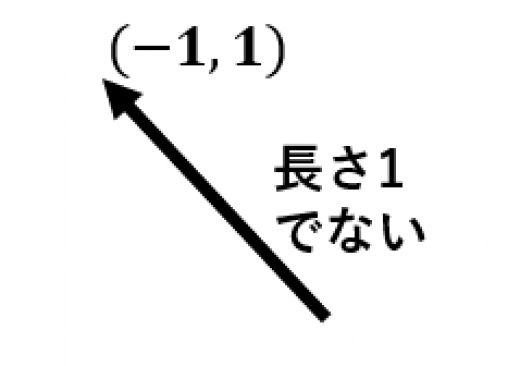
というベクトルは長さが なので単位ベクトルではありません。
単位ベクトルの求め方
単位ベクトルの求め方
ベクトル と同じ向きの単位ベクトルは
ベクトル をその長さ で割れば単位ベクトルになります。
と同じ向きの単位ベクトルを求めよ。
長さは, である。
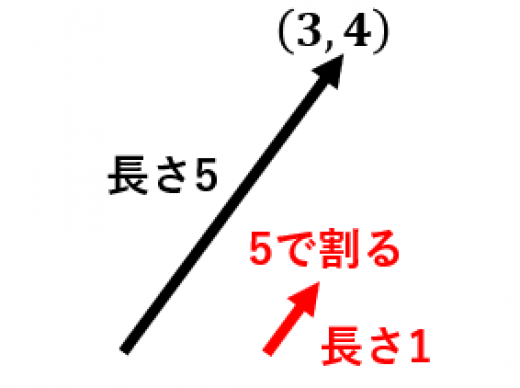 よって,求める単位ベクトルは の各成分を で割って,
よって,求める単位ベクトルは の各成分を で割って,
このように, というベクトルは,
- の定数倍なので, と同じ向きです。
- 自分の長さで割っているので,割った後の長さは1になります。つまり単位ベクトルです。
このように「同じ向き」で「長さを1にする」操作を正規化と言うことがあります。
平行な単位ベクトル
と平行な単位ベクトルを求めよ。
平行な単位ベクトルを計算する問題です!
同じ向きの単位ベクトルに加えて,同じ向きの単位ベクトルと逆向きのベクトルも平行な単位ベクトルになります。
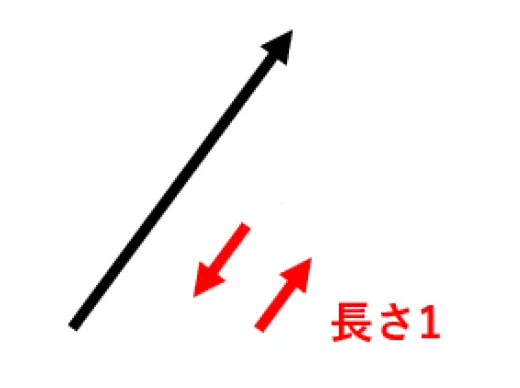
長さは, である。
よって, と平行な単位ベクトルは つまり, と である。
単位ベクトルの計算例
単位ベクトルの計算例
例題1では平面ベクトルについて考えましたが,空間ベクトルについても で自分と同じ向きの単位ベクトルを計算できます。
と同じ向きの単位ベクトルを求めよ。
より,求める単位ベクトルは
各成分が である 次元ベクトル と同じ向きの単位ベクトルを求めよ。
より,求める単位ベクトルは
余談: はいろいろなところに登場する重要なベクトルです。
単位ベクトルと内積
単位ベクトルと内積
単位ベクトルについて覚えておくべきこととして,内積との関係を載せておきます。
単位ベクトル と他のベクトル について,内積 は の 方向の成分を表す。
なす角を とすると だからです。
ベクトルを学びたての頃は単位ベクトルを求めて何が嬉しいんだって感じがしますが,正規化は数学や物理のあらゆる場面で登場します!











