中線定理の3通りの証明
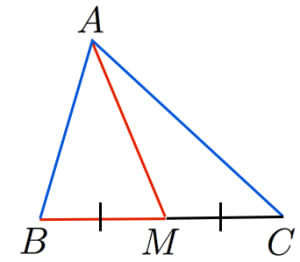
中線定理(パップスの中線定理)とは,図において が成立するという定理。ただし, は の中点。
中線定理の使用例
中線定理の使用例
三角形の「頂点」と「向かい合う辺の中点」を結ぶ線分 のことを中線と言います。中線定理を使えば,中線の長さを計算できます。
を の中点とし, とする。このとき の長さを求めよ。
中線定理より, つまり が成立する。よって となる。
→高校数学の問題集 ~最短で得点力を上げるために~のT41では,中線定理を使わない別解や「計算ミスを減らすコツ」も紹介しています。
中線定理の使い方
中線定理の使い方
さきほどの例題では,中線定理: を使って,3辺の長さから中線の長さを計算しましたが,他の使い方もあります。
中線定理を使えば「 の4つの長さのうち3つが分かれば残りの1つも簡単に分かる」と覚えておきましょう。
中線定理の証明の方針
中線定理の証明の方針
教科書にも載っている中線定理ですが,正弦定理や余弦定理などの花型公式と比べるとやや地味な感じがします。しかし,中線定理は様々な手法で証明できるので,図形の証明問題のよい題材です。
このページでは中線定理の証明を3通り紹介します。
- 余弦定理による方法
- ベクトルによる方法
- 座標平面による方法
証明1は発想を知らないと少し難しいかもしれませんが,重要な考え方です。証明2と3はベクトルや座標平面に慣れていれば機械的な計算で証明できます。
証明1:余弦定理による方法
証明1:余弦定理による方法
であることと余弦定理を用いて辺の関係式を導出します。
三角形 に余弦定理を用いると, 同様に,三角形 に余弦定理を用いると, ここで, と より,
これを整理すると中線定理となる。
非常に重要な考え方なので,この証明方法はまるごと覚えることをおすすめします!
証明2:ベクトルによる方法
証明2:ベクトルによる方法
ベクトルの計算で証明する場合は,始点をどこに取るかによって計算の複雑さが大きく変わります。この場合 を始点に取ると計算が楽になります。
とおくと, となる。
なので計算が楽です。一般に,中点や外心をベクトルの始点に取ると計算が楽になる場合が多いです。
証明3:座標平面による方法
証明3:座標平面による方法
ベクトルによる証明とほぼ同じですが,こちらも座標の取り方で計算の大変さが変わってきます。 を原点に取ると簡単に示せます。

と座標を設定する。
中線定理の左辺 は,
一方,中線定理の右辺は,
となり両辺は一致する。
ベクトルと同様,中点や外心を座標平面の原点にとるとうまくいく場合が多いです。
図形の証明問題
図形の証明問題
一般的に,図形の性質に注目して初等幾何で証明するのは発想力が必要になります。一方,ベクトルや座標平面による証明方法では機械的な計算で証明できますが,角度に関する条件を扱うのは難しいため万能ではありません,一長一短です。
どの手法を用いるのか,臨機応変に判断しなければいけません。
中線定理の応用例として三角形における距離の二乗の和の公式もどうぞ。
中線定理の逆
中線定理の逆
中線定理の逆は成立しません。つまり, 上の点 について, を満たしても が の中点とは限りません。簡単に反例を構成できます。
例えば証明3と同様に
とおき, とすると,
という条件から となります。
なら は中点ですが が のときも中線定理の式を満たします。
ベクトルと座標平面は本質的に同じです。ちなみに,中線定理を拡張したものにスチュワートの定理があります。
Tag:有名な定理を複数の方法で証明











