直線の方程式の一般形が嬉しい3つの理由
座標平面における直線の方程式には,いくつかの表し方がある。
- (傾きと切片による表現)
- (一般形)
直線の方程式の一般形について解説します。一般形が「傾きと切片による表現」よりも嬉しい理由を3つ紹介します。
直線の方程式の一般形
直線の方程式の一般形
1次関数 のグラフが直線になることは,中学数学で習います。 が傾きで, が切片です。
一方, 座標平面における直線は と表すこともできます。これを直線の一般形と呼びます。
という「傾きと切片による表現」は,移項することで と「一般形」で表すことができる。
では,なぜわざわざ一般形で表すのでしょうか? 「傾きと切片による表現」の方がイメージしやすく,一般形なんて必要ないのでは? ただ移項するだけじゃん? 私は高校生のときにそんな疑問を持っていました。
そこで,以下では直線の方程式の一般形が 「傾きと切片による表現」よりも優れている点を3つ紹介します。
先に3つの概要を述べると,以下のようになります:
- 一般形だと場合分けが不要
- 法線ベクトルによるイメージが嬉しい
- 高次元に拡張できるので嬉しい
一般形だと場合分けが不要
一般形だと場合分けが不要
傾きと切片による表現では, 軸に平行な直線を表すことができません。 などは直線ですが, という形では表せません。
一方,一般形 では, 軸に平行な直線も 軸に平行な直線もカバーできます。
つまり「全ての直線を統一的に扱える(場合分けがいらない)ので は嬉しい」と言えます。
法線ベクトルというイメージ
法線ベクトルというイメージ
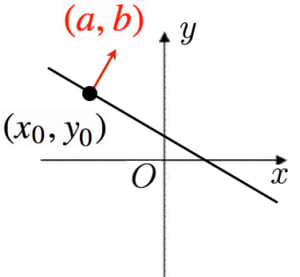
を通り と垂直な直線の方程式は,
ベクトル と が垂直⇔
より, 定数という形になっています。
つまり, は直線 の法線ベクトル(直線に垂直なベクトル)になっています。このイメージが非常に重要です。
直線の方程式 を作図するときに, について解いて作図してもよいですが, を通って ベクトル と垂直な直線と考えて作図することもできます。
このように,法線ベクトルのイメージを持っていれば,計算が楽になったり,しょうもないミスを防げることがあります。
直線の方程式が絡んだ問題では「傾きと切片のイメージ」と「法線ベクトルのイメージ」の両方を使えた方が見通しがよくなります。
つまり,「法線ベクトルによるイメージを提供してくれるので は嬉しい」と言えます。
3次元に拡張できる
3次元に拡張できる
は と に関して対称でないので,3次元に拡張することが難しいです。一方, は と に関して対称であり3次元に拡張しやすいです。
実際,上記の法線ベクトルの考え方を用いると,3次元空間座標における平面の方程式が導かれます:
空間座標においてベクトル に垂直な平面の方程式は適当な定数 を用いて,
と表すことができる。
定数 は平面が通る一点を代入することで決まります。
平面の方程式の公式は昔は高校範囲でしたが,最近は教科書に載っていないようです。しかし,空間座標の問題を解く際にしばしば役立つので覚えておくとよいです。→平面の方程式とその3通りの求め方
ちなみに, は, 次元に一般化できます。
次元直交座標においてベクトル に垂直な 次元超平面の方程式は,適当な定数 を用いて
と表すことができる。
つまり,「高次元に拡張できるので一般形は嬉しい」と言えます。
ちなみに,直線の表し方に関して,切片方程式という考え方もあります。→切片方程式とその証明に関すること
同じものを2通りで表して両方のメリットデメリットを考えると理解が深まります。











