写像12相(場合の数の有名問題)
更新
写像12相(Twelvefold way)と呼ばれる「場合の数」の有名問題を紹介します。
写像という言葉は知らなくても,高校数学の範囲で理解できます。
写像12相とは
写像12相とは
個の玉を
個の箱に入れる方法が何通りあるかを数えましょう。
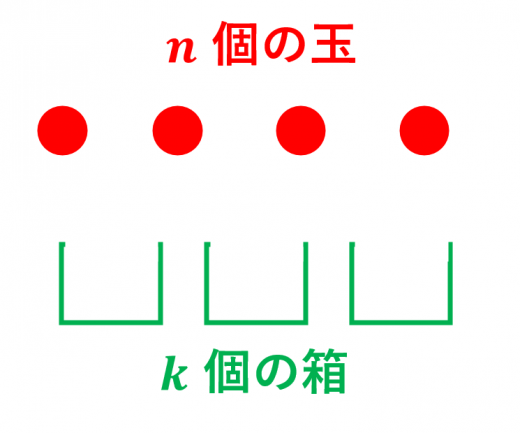
以下のように12パターンの問題設定が考えられます。
- 個の玉を区別する or しない
- 個の箱を区別する or しない
- 「条件なし」or「全ての箱の中身が1つ以下という条件つき」or 「全ての箱の中身が1つ以上という条件つき」
全部で パターンの問題があります。
まずは,12パターンのうちの1つを見てみましょう。
個の区別する玉を 個の区別する箱に入れる場合の数(条件なし)は 通りです。
これは簡単ですね。残りの11パターンも順番に考えていきましょう。以下の表の2~12を埋めるのが目標です。
| n個の玉 | k個の箱 | 条件なし | 各1つ以下 | 各1つ以上 |
|---|---|---|---|---|
| 区別する | 区別する | 2:易 | 3:難 | |
| 区別しない | 区別する | 4:普通 | 5:易 | 6:普通 |
| 区別する | 区別しない | 7:難 | 8:易 | 9:難 |
| 区別しない | 区別しない | 10:無理 | 11:易 | 12:無理 |
ただし,
- 玉が箱より多い場合「各1つ以下」を満たす入れ方は存在しません。よって,「各1つ以下」のパターンに関しては のもとで考えます。
- 同様に,箱が玉より多い場合「各1つ以上」を満たす入れ方は存在しません。よって,「各1つ以上」のパターンに関しては のもとで考えます。
では,残り11個頑張りましょう。難易度順に「2,5,8,11」→「4,6」→「3,7,9」→「10,12」と解説していきます。記事の最後に埋め終わった表があります。
単射の個数(易ゾーン)
単射の個数(易ゾーン)
まずは,「各1つ以下」という条件の場合(2,5,8,11)を考えます。同じ箱に2つ以上玉が入らないので簡単です。
-
2: 個の区別する玉を 個の区別する箱に入れる場合の数(全ての箱に一つ以下)は 通りです。
-
5: 個の区別しない玉を 個の区別する箱に入れる場合の数(全ての箱に一つ以下)は,玉を入れる箱を 個選ぶ場合の数なので 通りです。
-
8,11:箱を区別せず,全ての箱に一つ以下の場合, 個の玉を グループに分ける場合の数なのでただ1通りです。
仕切りで考える(普通ゾーン)
仕切りで考える(普通ゾーン)
次は区別しない玉を区別する箱に入れましょう。大学入試としては易しいレベルですが,重要な考え方です。
-
4: 個の区別しない玉を 個の区別する箱に入れる場合の数(条件なし)は, 個の玉と 個の仕切りを一列に並べる場合の数なので, 通り。
-
6:さらに,全ての箱に一つ以上という条件がある場合について。 個の玉を並べると玉と玉の隙間が 箇所できるが,その隙間から 個選んで仕切りを入れる場合の数なので, 通り。
詳しくは 重複組合せの公式と例題(玉,整数解の個数)で解説しています。4と6が難しかった人はぜひご覧ください。
全射の個数など(難ゾーン)
全射の個数など(難ゾーン)
3はかなり手強いです。3ができればそこから3→9→7とわかります。詳細は別記事で説明しています。→全射の個数の証明とベル数
-
3: 個の区別する玉を 個の区別する箱に入れる場合の数(全ての箱に1つ以上)は,
通りです(全射の個数を求める公式)。包除原理を用いて導出できます。 -
9:スターリング数と呼ばれる有名な数です。 個の箱を区別しない場合,3の場合を で割ったものになります:
-
7:ベル数と呼ばれる有名な数です。「各1つ以上」という条件が無いので9の場合を足し合わせます:
分割数(無理ゾーン)
分割数(無理ゾーン)
残る2つは分割数と呼ばれ, と の簡単な式で表す公式は見つかっていません。
-
12:玉も箱も区別せず,各1つ以上です。これは,正の整数 を 個の正の整数の和に分解する場合の数です。ここでは と書きます。
-
10:玉も箱も区別せず,条件なしです。これは,正の整数 を 個の非負の整数の和に分解する場合の数です。これは,正の整数 を 個の正の整数の和に分解する場合の数と等しく, となります。
や が小さい場合は入試などで出題されるかもしれませんが, に関する漸化式を立てるなり気合いで数えるなりするしかありません。→分割数の意味と性質・ヤング図形の活躍
写像12相まとめ
写像12相まとめ
| n個の玉 | k個の箱 | 条件なし | 各1つ以下 | 各1つ以上 |
|---|---|---|---|---|
| 区別する | 区別する | |||
| しない | する | |||
| する | しない | 1 | ||
| しない | しない | 1 |
なぜ写像12相というのか
なぜ写像12相というのか
- 個の玉をそれぞれをいずれかの箱に対応させる「写像」が何通りあるか数える問題です。
- 問題設定が12パターンあります。
写像12相という名前はかっこいいですね。
ちなみに,「各1つ以下」という条件は「単射」に対応し,「各1つ以上」という条件は「全射」に対応します。
私は難ゾーンの3マスが好きです。











