巡回セールスマン問題の意味と2近似アルゴリズム
離散最適化の有名問題である,巡回セールスマン問題(Traveling salesman problem, TSP)について。問題の意味と簡単な近似アルゴリズムについて解説します。
巡回セールスマン問題とは
巡回セールスマン問題とは
都市の数 と,二つの都市 と の間を移動するのにかかる時間 が与えられる。このとき,全ての都市を巡ってもとの都市に戻ってくるような経路のうち,移動時間が最小なものを求めよ。
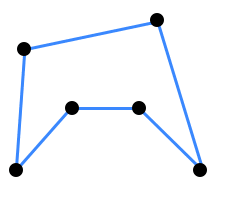
図は6都市の場合の例です(移動時間は図に書くのが難しいので,例えば二点間の距離と見てください)。青い経路はそれなりに合理的に見えますが,もっとよい経路があるかもしれません。
なお,グラフ理論の言葉を使うと「重み付きグラフに対して,重み最小のハミルトン閉路を求めよ」と述べることができます。
巡回セールスマン問題の難しさ
巡回セールスマン問題の難しさ
近似アルゴリズム
近似アルゴリズム
厳密な最適解を求めるのが難しいからと言ってそこで諦めてはいけません。厳密解が難しいので近似解を求めにいきましょう。
「最悪でも 倍」のような近似解が得られるとき,つまり,
近似アルゴリズムの出力解の値 本当の最適値
を満たすような解を出力してくれる近似アルゴリズムを 近似解法などと言います。
三角不等式を満たすTSP
三角不等式を満たすTSP
近似アルゴリズムを設計するために,問題に「移動時間が三角不等式を満たす」という仮定を加えます。
つまり,任意の に対して とします。
「寄り道した方が早いことはない」というのは現実的な仮定でしょう。なお,三角不等式を満たすTSPもNP-hardであることが知られています。近似解法が設計できると嬉しいです。
TSPの2近似解法
TSPの2近似解法
三角不等式を満たすTSPに対する2近似解法を解説します。
-
最小全域木 を求める。
-
の枝をコピーしたグラフを一筆書きで一周する。
-
一回通ったとこはショートカットすることで,全都市をちょうど一回巡る閉路にする。

注:最小全域木を求めるのは簡単です。例えばクラスカルのアルゴリズムという多項式時間解法があります。
注2: の枝をコピーしたグラフは全ての頂点の次数が偶数なので一筆書きで一周できます。→オイラーグラフの定理(一筆書きできる条件)とその証明
- の重み 真の最適値
- 2で得られる閉路の長さ= の重み
- 3で得られる閉路の長さ で得られる閉路の長さ
より,3で得られる閉路の長さ 真の最適値
ただし,三つ目の不等式で三角不等式を使った。
※2021/8/8追記:「2近似解法のことを2-opt法とも呼ぶ」という旨の誤った記載を消去しました。ご指摘いただきありがとうございました!
一般的なTSPに多項式時間近似解法がないことの証明
一般的なTSPに多項式時間近似解法がないことの証明
「移動時間が三角不等式を満たす」という条件をつけない場合は,P≠NPの仮定のもと,TSPに多項式時間の近似アルゴリズムがないことが証明できます。つまり,どのような定数 に対しても 近似解法は存在しません。
証明には,ハミルトン閉路があるかどうかを判定する問題「ハミルトン閉路問題」を使います。
TSPの 近似解法が存在すると仮定して,矛盾を導く。概要は以下の1~3。
- 任意のグラフ に対して,下図のようにグラフ を作る。
- TSP の多項式時間 近似解法を に適用すると, のハミルトン閉路問題が多項式時間で解ける。
- ハミルトン閉路はNP-completeなので矛盾。
-
の詳細
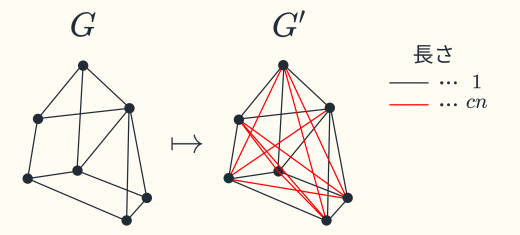 の頂点をそのままで,完全グラフにしたものを とする。ただし, の枝の長さは,もともと に枝があった場合 ,もともと には枝がなかった場合長さ とする。ここで, は の頂点数。
の頂点をそのままで,完全グラフにしたものを とする。ただし, の枝の長さは,もともと に枝があった場合 ,もともと には枝がなかった場合長さ とする。ここで, は の頂点数。 -
2の詳細
以下のように,TSPの答えから のハミルトン閉路の有無が確認できる。- もし, にハミルトン閉路があった場合, をTSPでとくとその閉路が最短の経路になり,長さは になる。
- 逆に, にハミルトン閉路がなかった場合, をTSPでとくと,経路のうち必ず1本は長さ のものが入るので,最短の経路の長さは 以上になる。
-
3について,ハミルトン閉路問題はNP-completeであることの証明は省略します。
ちなみに,三角不等式を満たすTSPに対してはマッチングを用いた1.5近似アルゴリズムもあります。マッチング素晴らしいですね。











