等差数列の和
等差数列とは,同じ数ずつ増えていく(または減っていく)数の列のことです。
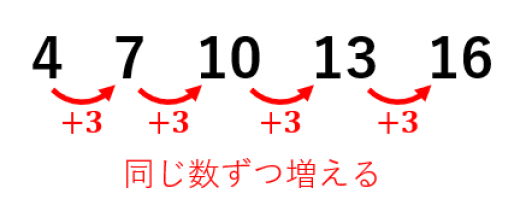
等差数列の基礎と和の公式についてわかりやすく説明します。
等差数列の例
等差数列の例
は ずつ増えていく等差数列です。
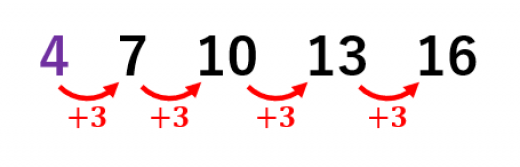
等差数列において,最初の数を初項,増えていく一定値のことを公差,並んでいる個数を項数と言います。
は 初項が で 公差が で 項数が である等差数列です。
以下の等差数列の初項・公差・項数を述べよ。
-
は 初項が で 公差が で 項数が である等差数列。
-
は 初項が で 公差が で 項数が である等差数列。
等差数列の和
等差数列の和
同じ数ずつ増える(減る)数たちの足し算は
で計算できる。
を計算せよ。
同じ数ずつ増える数たち(等差数列)の足し算である。
- 最初の数は
- 最後の数は
- 個数は
なので,公式を使うと
等差数列の和の公式の証明
まずは具体例で, について考えてみます。
図を見てください。
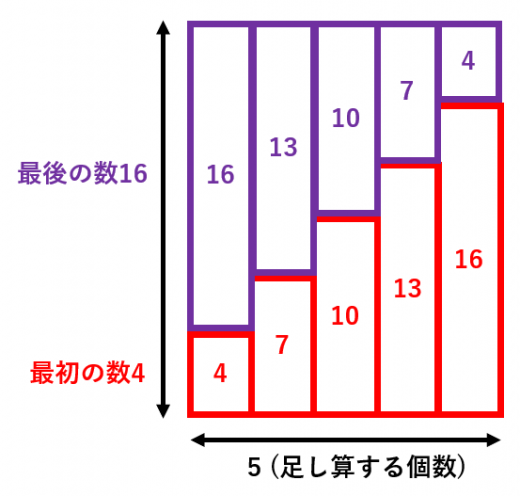
を赤と紫で2つ並べると,大きな長方形になります。
- 長方形の縦の長さは
- 横の長さは
よって,長方形の面積は になります。結局求める足し算の答えは になります。
一般の場合も になることがわかります。
和の公式の覚え方と練習問題
という公式について,
-
平均値 に個数 をかけたものと覚えるとおぼえやすいです。
-
台形の面積公式:(上底+下底)×高さ÷2 と似ていることからも覚えやすいです。
-
あとは,多くの練習問題を解いて覚えましょう。
- (1) を計算せよ。
- (2) 以下の偶数の和を求めよ。
(1) 最初,最後,個数 として等差数列の和の公式を使うと,
(2) を計算すればよい。
最初,最後,個数 として等差数列の和の公式を使うと,
等差数列の一般項
等差数列の一般項
等差数列において,初項を ,公差を とすると, 番目の数 は
と表せる。
という等差数列では, なので 番目の数は
つまり と表せる。
例えば とすると である。たしかに3番目の数は になっている。
- 等差数列では番号が1進むごとに数が 増えます。 番目は最初の数から「 回だけ」 増えるので となります。
- 番目の数 を の式で表すことを「一般項を求める」と言います。
以下の等差数列の一般項を求めよ。
-
は初項が で公差が なので,一般項は
-
は初項が で公差が なので,一般項は
補足
補足
等差数列の和に関する2つの補足です。
和の公式の別の形
等差数列の和は
で計算できましたが。「最後の数」ではなく項数 を使って表す公式もあります。
初項が ,公差が ,項数が であるような等差数列の和は,
これは覚える必要はありません。和の公式 に,一般項の式 を代入するだけですぐに導けます。
初項が ,公差が ,項数が であるような等差数列の和 を求めよ。
和の公式 において とすると,
発展:自然数の和の公式
自然数の和の公式だけ覚えていれば等差数列の和の公式を瞬時に導出できます!
つまり,等差数列の和の公式は自然数の和の公式と似たようなもの(1次変換しただけ)というわけです。
教科書レベルの公式を解説するときも.教科書に載っていないような視点,ネタを提供できるように頑張りたいです。











