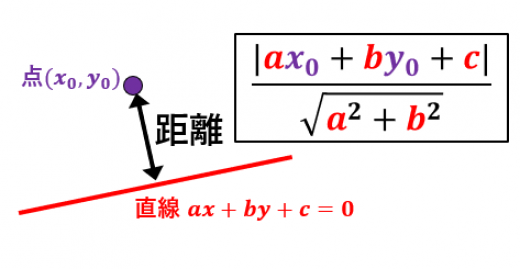
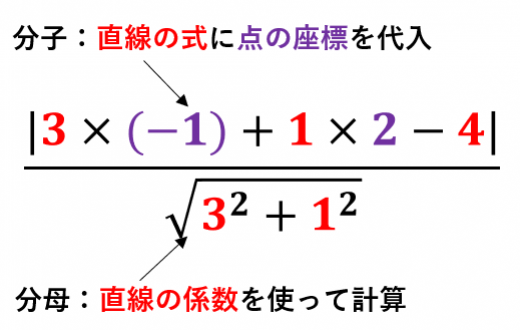
点と直線の距離公式の証明を5通り紹介します。以下では,点の座標を A(x0,y0) 直線を l:ax+by+c=0 とします。点から直線におろした垂線の足を H とします。
AH=a2+b2∣ax0+by0+c∣ の導出が目標です。
1. ひたすら座標計算する証明
中学数学の範囲で理解できます。難しい発想は必要なく,H の座標を求めてひたすら計算するだけです。
証明
直線:ax+by+c=0 を変形すると,
y=−bax−bc
となり傾きは −ba である。
よって,これに垂直な直線の傾きは ab である(垂直なら傾きの積が −1 なので)。
よって,垂線 AH は,(x0,y0) を通り傾き ab の直線なので,y=ab(x−x0)+y0
次に,垂線ともとの直線の交点である H の座標を求める:
−bax−bc=abx−abx0+y0
計算していくと,
−a2x−acx=b2x−b2x0+aby0=a2+b2b2x0−aby0−ac
y 座標は
−bax−bc=a2+b2−abx0+a2y0+ba2c−ba2c−bc=a2+b2−abx0+a2y0−bc
あとは,AH=(x−x0)2+(y−y0)2 を計算するだけ:
x−x0=a2+b2−a(ax0+by0+c)y−y0=a2+b2−b(ax0+by0+c)
より,
AH=a2+b2∣ax0+by0+c∣(−a)2+(−b)2=a2+b2∣ax0+by0+c∣
x−x0,y−y0 がきれいな式になるのがおもしろいです。
2. ベクトルを使う証明1
次は「法線ベクトル」という高校数学の知識を使う証明です。つまり,ax+by+c=0 という直線とベクトル (a,b) は垂直になるという性質を使います。→法線ベクトルの3通りの求め方と応用
これを使えば,H
の座標を求めずに計算できるので証明1より計算が楽です。
証明
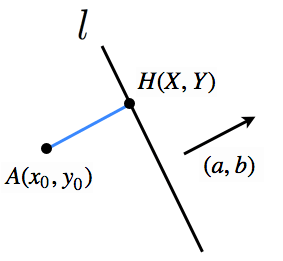
H
の座標を
(X,Y)
とする。
AH
は
l
の法線ベクトルと平行なので実数
t
を用いて,
(X−x0,Y−y0)=t(a,b)
と表せる。あとは,H
が
l
上にある条件:
aX+bY=−c
を用いて
t
を求めればOK。
上式の両辺に対して
(a,b)
との内積を取ると,
a(X−x0)+b(Y−y0)=ta×a+tb×b
である。これと
aX+bY=−c
より,
−c−ax0−by0=t(a2+b2)
となる。
a2+b2=0
なので,
t=−a2+b2ax0+by0+c
よって,AH
の長さ,すなわち
t(a,b)
の長さは,
d=∣t∣a2+b2=a2+b2∣ax0+by0+c∣
となり点と直線の距離公式が証明された。
3. ベクトルを使う証明2
法線ベクトルに加えて「正射影ベクトル」という道具を用いた証明を紹介します。本質的には2番目の証明と同じですが,よりシンプルに証明を書くことができます。→ 正射影ベクトルの公式の証明と使い方
証明
l 上の任意の点 B の座標を B(x1,y1) とおく。H の座標を (X,Y) とする。
法線ベクトルを n とおく。n=(a,b) である。
AH は AB の n への正射影ベクトルであるため
AH=∣n∣2AB⋅nn
である。この絶対値を計算すればよい。
∣AH∣=∣n∣∣AB⋅n∣=∣n∣∣(OB−OA)⋅n∣=a2+b2∣ax1+by1−ax0−by0∣=a2+b2∣ax0+by0+c∣
となる。なお,最後の計算では B が l 上にあることから ax1+by1+c=0 となることを用いた。
4. 三角形の面積を用いた証明
三角形の面積を二通りの方法で表すことで,距離公式を導出します。おもしろい方法です。
証明
a=0
のとき,直線
l
は
y=−bc
となるので求める距離は
∣y0+bc∣
となり距離公式は正しい。
b=0
のときも同様。よって,以下
a,b
ともに
0
でない場合を考える。

l
上に点
P,Q
を「
P
と
A
の
x
座標が等しく,Q
と
A
の
y
座標が等しくなる」ようにとる。
PA=p,QA=q
とおくと,PQ=p2+q2
である。
三角形の面積を二通りの方法で表すことにより,
21pq=21dp2+q2
つまり,d=p2+q2pq
を得る。
直線の方程式を利用して
P
の
y
座標を求めることにより,
p=∣∣b−c−ax0−y0∣∣=∣b∣1∣ax0+by0+c∣
同様に,
q=∣∣a−c−by0−x0∣∣=∣a∣1∣ax0+by0+c∣
となるので,これらを上式に代入して整理すると
d=a2+b2∣ax0+by0+c∣
が得られ,点と直線の距離公式が証明された。
5. 点を動かすことによる証明
d
を
x0
と
y0
の関数とみなし,関数を決定していくという方法です。
証明
l
を固定したとき,A
の場所によって
d
が決まるので,d
は
x0
と
y0
の関数とみなせる。
まず
ax+by+c≥0
の領域に
A
がある場合を考える。

A
を
x
軸方向に変化させたときの
d
の変化量は
x0
の変化量に比例するので
d
は
x0
の一次関数。同様に
y0
の一次関数でもある。
よって,d=αx0+βy0+γ
と書ける。
x0
を
a2+b2
ずらすと
d
は
a
ずれるので,
α=a2+b2a
同様に,
β=a2+b2b
また「ax0+by0+c=0
のとき
d=0」という状況を,
d=αx0+βy0+γ=a2+b2ax0+by0+γ
に代入すると,
γ=a2+b2c
よって,
d=a2+b2ax0+by0+c
また,ax+by+c≤0
の領域に
A
がある場合も同様に,
d=−a2+b2ax0+by0+c
となるので点と直線の距離公式が証明された。
このように点と直線の距離公式の証明1つでもいろいろな方法が考えられます。座標の問題に対する様々なアプローチの勉強になります。
Tag:有名な定理を複数の方法で証明
Tag:数学2の教科書に載っている公式の解説一覧