底の変換公式の証明と例題
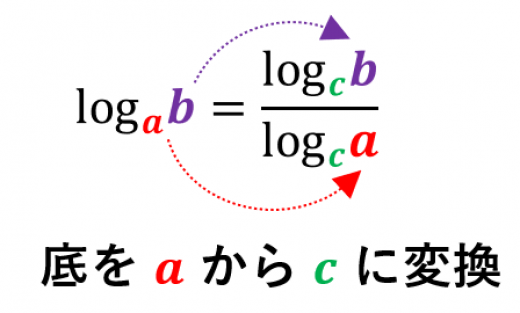
, のとき
底の変換公式について,意味と証明を解説します。
底の変換公式とは
底の変換公式とは
- 対数 について, の部分を底と言います。
- 底を ではなく に変換したい! という場合があります。
- そんなときに使えるのが,以下の底の変換公式です:
左辺では底が ですが,右辺では に変換されています。
の底を に変換して計算せよ。
として底の変換公式を使うと,
となり底が になった。, なので,右辺は になる。
底の変換公式の証明
底の変換公式の証明
底の変換公式
を証明してみましょう。証明に使うのは,以下の2つです。
- 対数の定義:
とは を満たす のこと - 対数の性質:
「 を満たす実数 を とする」というのが対数の定義であった。
つまり, が成立する。
両辺の対数を取る(底は )と,
ここで,対数の性質: を用いて左辺を変形すると以下を得る。
両辺を で割ると底の変換公式を得る。
底の変換公式の使い方のコツ
底の変換公式の使い方のコツ
-
底の変換公式:
を使うと,対数の底を から に変換できます。そのため,底の変換公式は,対数の底をそろえるために使われます。 -
底の決め方(いくつにそろえるか)で迷う人がいますが,後述の例題で見るように底はなんでもOKです。
底の変換公式を使う例題
底の変換公式を使う例題
を計算せよ。
底の変換公式を使って底を にするのがスタンダードな考え方。
底は である必要はない。なんでもよい。
注:慣れていれば普通に より ,と一瞬で計算できます。
を計算せよ。
例えば底を にそろえるのがスタンダードな考え方。
底は である必要はない。なんでもよい。
なお,覚えておきたい対数(log)の応用公式4点セットの公式(ii)を使えば一発で
が分かります。
→高校数学の問題集 ~最短で得点力を上げるために~のT19で,この記事の復習をしてみてください。
底の変換公式は,底の「」という変換です。 がなんでも良いというのが面白いです。










