放物線の準線・焦点と一般化
更新
直線 と点 からの距離が等しい点の集合は放物線である。 をこの放物線の準線, を焦点と呼ぶ。
軌跡に関する基本的な知識であり,二次曲線の基本的な公式でもあります。
前半は教科書レベル,後半はこの公式のある種の一般化です。
準線と焦点から放物線を導出
準線と焦点から放物線を導出
以下 とします。
準線 ,焦点 に対して,準線と焦点からの距離が等しい点の集合は放物線 全体となる。
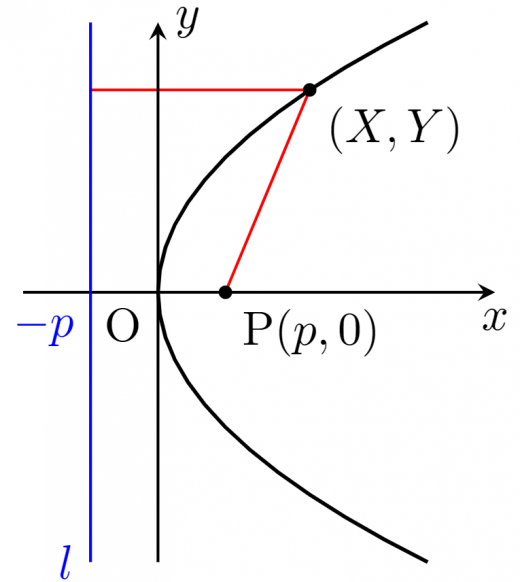
点 と準線の距離は,,焦点との距離は, である。
これらが等しいことの必要十分条件は,
である。これを整理すると,
となる。
「放物線の式」と「焦点,準線」の行き来
「放物線の式」と「焦点,準線」の行き来
さきほどの結果は様々な言い換えができます。以下の公式を覚える必要はありませんが,さきほどの結果からすぐに導出できるようになっておきましょう。
- 放物線から準線と焦点を求める
放物線 の準線は ,焦点は である。
- と を交換
直線 と頂点 からの距離が等しい点の軌跡は,放物線: である。
- 以上2つの合体
放物線 の準線は ,焦点は である。
円と直線に接する点の軌跡
円と直線に接する点の軌跡
軌跡に関するそれなりに有名な事実です!
-
直線 に接し,円 と外接するような円の中心の軌跡は放物線である。
-
直線 に接し,円 を内側に含み,円 に内接するような円の中心の軌跡は放物線である。
円 の半径をどんどん小さくしていき の極限を考えると冒頭の主張が得られます。すなわち,この定理2は冒頭の主張のある種の一般化になっています。
2も同様なので1だけ証明します。

とおいても一般性を失わない。
が求める軌跡上にある
を移項して両辺に二乗すると,(注:ここの変形は のもとで必要十分)
となり,整理すると
となり,放物線上にあることが分かる。
注:上記で証明したのは厳密には必要条件のみですが,十分条件(軌跡が放物線 全体を動くこと)も簡単に確認できます。つまり,放物線上にあるとき を言えばOKです。
定理1を用いて証明することもできます。
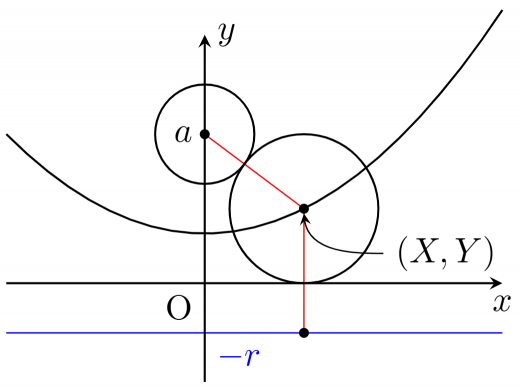
同じく,
とおいても一般性を失わない。図の青い直線 を考えると,求める軌跡は, と からの距離が等しい点の集合である。これは,定理1より放物線である!
これで定理2の証明は完了だが,実際に放物線の式を計算してみる。
図全体を 方向に 平行移動すると,放物線は を焦点, を準線とする放物線に移る。
移った先の放物線の式は すなわち となる。
これを元に戻す( 方向に 平行移動する)ことで を得る。
軌跡の問題では十分性の確認を忘れやすいので注意しましょう。











