垂心の存在の3通りの証明
どんな三角形でも,各頂点から向かいの辺に下ろした3本の垂線は一点で交わる。その点を三角形の垂心と呼ぶ。
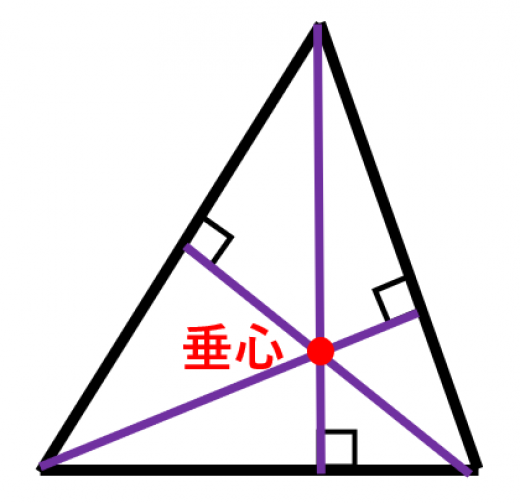
三角形の垂心について,垂心が存在することの3通りの証明を紹介します。
- 外心の存在を用いた証明
- 外心の存在を用いた証明
まずは1つめの証明です。三角形の外心については前提知識とします。つまり,三角形において,各辺の垂直二等分線は1点で交わるという定理を使います。
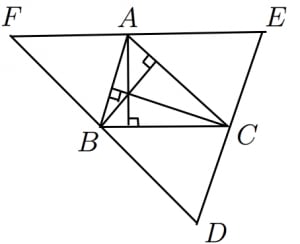
三角形 の各頂点を通り対辺と平行な直線を3つ引き,それらの交点を とおく。
まず,三角形 と は合同である。なぜなら,以下のように1辺とその両端がそれぞれ等しいから:
- 平行線の錯角より
- 平行線の錯角より
- は共通
同様に考えると,4つの小さい三角形 はすべて合同である。特に,。 よって,
- 「 から におろした垂線」=「 の垂直二等分線」
同様に,
- 「 から におろした垂線」=「 の垂直二等分線
- 「 から におろした垂線」=「 の垂直二等分線」
ここで, 三角形 において,3辺の垂直二等分線は1点で交わるので, における3本の垂線も1点で交わる。以上により垂心の存在が証明された。
- チェバの定理の逆を用いた証明
- チェバの定理の逆を用いた証明
証明2では,チェバの定理の逆を使います。チェバの定理の逆については,チェバの定理:例題と3通りの証明を参考にしてください。

垂線の足を とおくと,
より,
よって,チェバの定理の逆より, は1点で交わる。つまり,垂心が存在する。
- 座標を用いた証明
- 座標を用いた証明
3本の直線が1点で交わることを,直交座標を用いて証明します。垂線の1つと 軸が一致するように座標を設定すると計算が楽になります。

角 が最大角としても一般性を失わない。
と座標を設定する
の傾きは より,直線 の方程式は,
これと, 軸との交点の 座標は,
同様にして(または対称性より), も を通る。 よって, はすべて を通る。よって,垂心の存在が証明された。
注: が最大角という条件を指定することで となり傾きが定義できます。
垂直が多い構図では座標で計算するのがうまくいく場合が多いです。











