sinを用いた三角形の面積公式

更新 2021/03/07

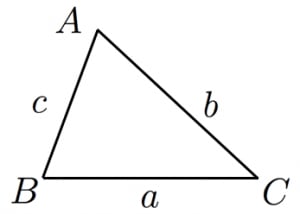
sinmenseki

三角形 $ABC$ の面積 $S$ は，

$S=\dfrac{1}{2}ab\sin C=\dfrac{1}{2}bc\sin A=\dfrac{1}{2}ca\sin B$

教科書に載っている非常に基本的な公式です。前半はこの公式を使う例題および証明です。後半は他の公式との関係について考えます。

具体例

二辺とその間の角が分かれば面積が求まります！

例題1

$BC=3$ ， $CA=4$ ， $C=30^{\circ}$ である三角形の面積 $S$ を求めよ。

解答

$\sin 30^{\circ}=\dfrac{1}{2}$ なので，面積公式より，

$S=\dfrac{1}{2}\cdot 3\cdot 4\cdot \sin 30^{\circ}=3$

三辺の長さが与えられているときは（ヘロンの公式を用いてもよいですが），余弦定理を用いてコサインを求めてからサインを求めます。

例題2

$BC=5$ ， $CA=6$ ， $AB=7$ である三角形の面積 $S$ を求めよ。

解答

余弦定理より，

$\cos C=\dfrac{5^2+6^2-7^2}{2\cdot 5\cdot 6}=\dfrac{1}{5}$

これと $\sin^2 C+\cos^2 C=1$ より

$\sin C=\sqrt{1-\cos^2 C}=\dfrac{2\sqrt{6}}{5}$

よって，面積公式より，

$S=\dfrac{1}{2}\cdot 5\cdot 6\cdot \dfrac{2\sqrt{6}}{5}=6\sqrt{6}$

公式の証明

$S=\dfrac{1}{2}ab\sin C$ についてのみ証明します。残り2つは対称性から分かります。

証明

サインを用いた面積公式の証明

$BC$ を底辺と見ると，

底辺 $=a$

高さ $=b\sin C$

となるので，面積は，

底辺×高さ÷ $2=\dfrac{1}{2}ab\sin C$

（鋭角三角形の場合と鈍角三角形の場合で図は異なるが，いずれの場合も上記の議論は正しい）

面積公式から分かること

角を1つ共有する2つの三角形の面積比は，その角を作る2辺の長さの積の比に等しいことが分かります。つまり，図において，
△
ABC:ABC:ABC:
△
ADE=AB⋅AC:AD⋅AEADE=AB\cdot AC:AD\cdot AEADE=AB⋅AC:AD⋅AE
が成立します。
→三角形の面積比にまつわる公式たち
特に，相似な三角形の面積比は相似比の二乗に比例することも分かります。
→相似比と面積比・体積比：いろいろな例と証明
また，サインの性質：
sin⁡θ=sin⁡(180∘−θ)\sin \theta=\sin (180^{\circ}-\theta)sinθ=sin(180∘−θ)
 に注意すると，円に内接する四角形
ABCDABCDABCD
 において，
△
ABC:ABC:ABC:
△
ADC=AB⋅BC:AD⋅DCADC=AB\cdot BC:AD\cdot DCADC=AB⋅BC:AD⋅DC
であることも分かります。
→円に内接する四角形の性質とその証明まとめ

他の面積公式との関係

この面積公式をもとに他の面積公式を導出することができます。

例えば，この公式と正弦定理を用いることで対称な式： $S=\dfrac{abc}{4R}$ を得ることができます（ $R$ は三角形 $ABC$ の外接円の半径）。→外接円の半径と三角形の面積の関係

また，余弦定理を用いて角度の情報を辺の情報に変換することでヘロンの公式： $S=\sqrt{s(s-a)(s-b)(s-c)}$ を得ることができます。→ヘロンの公式の証明と使用例

$2015=5\cdot 13\cdot 31$ 年もあと少しですね。もうすぐ $2016=2^5\cdot 3^2\cdot 7$ 年ですね。

Tag:数学１の教科書に載っている公式の解説一覧

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！