sinc 関数：sinx/x について覚えておくべきこと

更新 2023/05/05

sinc関数

$y=\dfrac{\sin x}{x}$ は sinc 関数と呼ぶ。

有名関数 $y=\dfrac{\sin x}{x}$ という関数に関連する話題を整理しました。

sinx/x の極限

$\lim_{x\to 0}\dfrac{\sin x}{x}=1$

まずは $\dfrac{\sin x}{x}$ の極限です。非常に有名な公式です。

証明

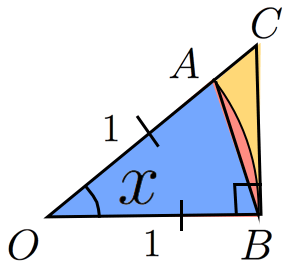
sinx/xの極限

図において面積に以下の不等式が成立する： $\text{三角形} \ \mathrm{OAB} < \text{扇形} \ \mathrm{OAB} < \text{三角形} \ \mathrm{OBC}$ すなわち， $\dfrac{1}{2}\sin x < \dfrac{1}{2}x < \dfrac{1}{2}\tan x$ となる。両辺を $\sin x$ で割って逆数をとる： $\cos x < \dfrac{\sin x}{x} < 1$

ここで， $x \to +0$ とすると， $\cos x\to 1$ なのではさみうちの原理から $\displaystyle\lim_{x\to +0}\dfrac{\sin x}{x}=1$ である。

また， $\dfrac{\sin x}{x}=\dfrac{\sin (-x)}{-x}$ なので， $\displaystyle\lim_{x\to -0}\dfrac{\sin x}{x}=1$ となる。

以上から，

$\lim_{x\to 0}\dfrac{\sin x}{x}=1$

である。

証明の補足

上記の導出方法は有名なので覚えておくとよいでしょう。
図形的性質が使えるのは $x > 0$ の場合だけなのでまわりくどいですが $x \to -0$ の場合も証明しました。
2013年の阪大理系でそのまま出題されています。
$\sin x < x$ は $\sin x$ を上からおさえる公式ですが，下からおさえる有名な不等式もあります。→ジョルダンの不等式とその3通りの証明

sinx/xの拡張

f(x)=sin⁡xxf(x) = \dfrac{\sin x}{x}f(x)=xsinx​ という関数は，厳密には x=0x = 0x=0 で定義されていません。
前述の極限を踏まえると，x=0x = 0x=0 で連続になるよう拡張ができます。これを sinc 関数（シンク関数）といい
sinc (x)={sin⁡xx(x≠0)1(x=0)
\mathrm{sinc}\ (x) 
=\begin{cases}
\dfrac{\sin x}{x} &(x\neq 0) \\
1 &(x=0)
\end{cases}
sinc (x)=⎩⎨⎧​xsinx​1​(x=0)(x=0)​
と定義します。

sinc 関数の微分とグラフ

グラフ

$y=\dfrac{\sin x}{x}$ のグラフを素早く書く方法を紹介します。

より，一般に $y=f(x)\times\sin x$ のグラフは以下の3段階の手順でかけます！

1. $y=f(x), y=-f(x)$ のグラフをかく

$x=n\pi$ ( $n$ は整数)と $x$ 軸の交点に点を打つ。

3. $\sin x$ のグラフを伸縮させながらかく

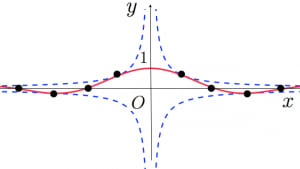
sinc関数のグラフ

$y=\dfrac{\sin x}{x}$ の場合， $f(x)=\dfrac{1}{x}$ です。上記の手順に従ってグラフをかいてみました。

面倒な微分計算，増減表は必要ありません！この方法はぜひマスターしてください。

$y=e^x\sin x,y=e^x\cos x$ なども同様にして簡単にグラフをかくことができます。

微分

$y=\dfrac{\sin x}{x}$ の導関数は $y'=\dfrac{x\cos x-\sin x}{x^2}$

証明

商の微分公式より， $\dfrac{\sin x}{x}$ の微分は

$\dfrac{\cos x\times x-1\times\sin x}{x^2}=\dfrac{x\cos x-\sin x}{x^2}$ となる。

単調性

定理

$0<x<\dfrac{\pi}{2}$ で $\dfrac{\sin x}{x}$ は単調減少

証明

$y'=\dfrac{x-\tan x}{x^2\cos x}$

だが， $0<x<\dfrac{\pi}{2}$ で $x<\tan x$ より $y'<0$ よって， $0<x<\dfrac{\pi}{2}$ では $\dfrac{\sin x}{x}$ は単調減少

sinc 関数の積分

sinc 関数を $0$ から $\infty$ まで積分すると有限値を取ります。

$\int_0^{\infty} \dfrac{\sin x}{x} dx = \dfrac{\pi}{2}$

ディリクレ積分と呼ばれます。証明は様々な方法があります。→ 留数定理を用いた三角関数の積分

sinc関数は信号処理などの工学的な応用もある有名な関数です。入試問題を作るのは大学の先生たちで，適当な関数を持ってくるよりも，工学的に意味を持つ関数を出題する可能性の方が高いと思われます（個人的な予想）。

Tag:大学入試で頻出の有名な関数まとめ

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！