(k,n)しきい値法とシャミアの秘密分散法
多項式補間を使うことで「故障に強い」かつ「漏洩に強い」秘密情報の保管が実現できる。
しきい値法の意味・嬉しさについて説明し,それを具体的に実現する方法としてシャミアの秘密分散法を解説します。
秘密分散法と(k,n)しきい値法
秘密分散法と(k,n)しきい値法
秘密分散法とは,隠したい情報をいくつかに分割してばらばらに保存しておく方法のことです。
特にこの記事では しきい値法というものを考えます。
- 秘密情報を 個に分割する(分割したものをシェアと言う)
- そのうち 個を使えば秘密情報が復元できるようにしておく
- 個以下だと秘密情報が復元できないようにしておく
しきい値法の例です:
-
秘密情報を3つに分割して東京,大阪,北海道に置いておく。
-
二つ使えば秘密情報が復元できる(三つのデータのうち一つ壊れても復元できる!)
-
一つだと秘密情報が復元できない(一つ盗まれても大丈夫!)
このように, しきい値法は 「故障に強い」かつ「漏洩に強い」という素晴らしい方法なのです。
シャミアの秘密分散法
シャミアの秘密分散法
しきい値法を具体的に実現する方法としてシャミア(Shamir)の秘密分散法を紹介します(よく分からない場合は後述の例参照)。
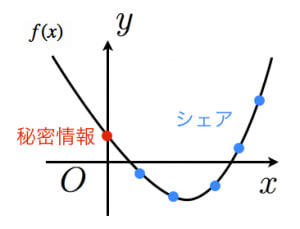
〜秘密分散の実現〜
- 秘密情報を とする
- 定数項が である 次多項式 を適当に作る
- 通る点の座標 をシェアとする
〜復元方法〜
個以上のシェアが手元にある
→
が通る点が
個以上分かる
→多項式補間により
が分かる(→注)
→秘密情報
を特定できる
注: 点を通る 次多項式は一つに決まります。→二次関数の決定とその背景
〜漏洩に強いこと〜
個以下の通る点からは は分からない。秘密情報 に関する情報は全く得られない。
具体例
具体例
具体例として しきい値法をやってみます。秘密情報は7とします。
〜秘密分散の実現〜
定数項が である 次多項式を適当に作る:
通る点 をシェアとする。
〜復元方法〜
三つのシェアのうち二つ,例えば と が分かれば,その2点を通る直線の方程式 が求まる。つまり秘密情報 が復元できる。
〜漏洩に強いこと〜
一つのシェアがバレても,通る一点からは直線は特定できない(切片に関する情報は全く得られない)ので秘密情報は守られる。
補間で保管











