握手の補題とエルデシュガライの定理

点（頂点）を線（辺，枝とも呼ぶ）で結んだものをグラフと言い，ある頂点から出ている辺の本数をその頂点の次数と言います。

全ての枝には端点が二つあるので，次数として二回カウントされます。そのため，握手の補題が成り立つのは明らかです。

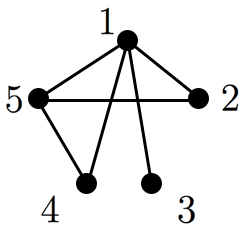
例えば図のグラフ（図内の数字は頂点番号を表す）において，$d_1=4,\:d_2=2,\:d_3=1,\\d_4=2,\:d_5=3$

となり，全ての次数の和は枝数 $6$ の二倍となっています。

握手の補題から以下のようなことも言えます。

主張2：特に，グラフの次数の総和は偶数

主張3：次数が奇数であるような頂点の数は偶数個

いずれも大した主張ではありません，知らなくても簡単に導けます。しかし，数オリの問題やグラフ理論に関する定理の証明ではときどき握手の補題の考え方を使うので知っておくとよいでしょう。

例えば，2001年JMO本選第1問は握手の補題を「主張3」の形で使うことで一発で解けます。 →JMO本選2001問題（数オリ財団のページです）

「次数の総和が偶数」というのは当たり前でしたが，グラフの次数には他にも条件があります（多重辺や自己ループはないものとします）。

それは大雑把にいうと「グラフの次数は偏り過ぎていない」という条件です。例えば頂点数が $4$ で次数が $3,3,1,1$ というグラフは（次数の和は偶数ですが）絶対に作れません。

一般的に，グラフの次数を大きい順に $d_1,\:d_2,\cdots,\:d_n$ とおくとき，任意の $k$ に対して以下の条件が満たされています。

$\displaystyle\sum_{i=1}^kd_i\leq k(k-1)+\sum_{i=k+1}^n\mathrm{min}(d_i,k)$

（$\mathrm{min}(a,b)$ は $a$ と $b$ のうちの小さい方を表す）

これは頂点 $1$ から $k$ までをひとグループと見ると理解できます。

• 左辺はグループに属する頂点たちの次数の和です。
• 右辺第一項：グループ内の枝の本数は最大で $\dfrac{k(k-1)}{2}$ 本なのでグループ内で消費できる次数は最大で $k(k-1)$ です→青色の枝。
• 右辺第二項：グループ内の頂点とグループ外の頂点 $i$ を結ぶことで消費できる次数の数は $d_i$ と $k$ のうちの小さい方となります（$d_i$ が $k$ 以上なら $k$ 個全部と結べるが→緑色，小さいときには $d_i$ 個としか結べない→赤）。

（自己ループ，多重辺がない）グラフが与えられたときにその次数を降順に並べた列 $d_1,\:d_2,\cdots,\:d_n$ が満たすべき式が二つ導出できました。逆に，この二つの条件を満たせばそのような次数列を持つグラフが必ず構成できるのです！

必要性の証明は今までの議論で終わっていますが，十分性の証明はかなり難しいです。