正八面体を上から見た図と東大の問題
正八面体を上から見た図と,1つの面と平行な平面で切った切断面の形は覚えておくとよい。
正八面体を上から見た図
正八面体を上から見た図
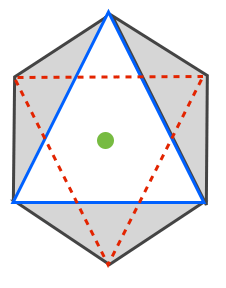
正八面体の一つの面が水平になるように地面においたときに,上から見た図はこのようになります。青い三角形が底面,赤い三角形が天面(見ている人に一番近い面)緑の点は底面および天面の重心に対応する点です。
空間把握能力が高ければこの図をイメージするのは簡単ですが,東大入試では過去2回も出題されているので覚えておきましょう。
図がこのようになる理由は「対称性より」と書けば十分です。納得しきれない人はぜひ正八面体を作ってみてください。
正八面体を底面に平行な平面で切断した図
正八面体を底面に平行な平面で切断した図
こちらも重要です。

正八面体を底面に平行な平面で切断すると六角形 ができます。対称性より かつ が成立します。
さらに,正八面体の一辺の長さを とすると, であることが分かります。
この性質は,さきほどの上から見た図で考えれば説明することができます。紫の点線が切断面を表しています。

この図を利用して として の長さを求めると, であることが分かります。
ちなみに は展開図で考えても,座標空間で考えても導出することができます。
1990年東大理系第3問
1990年東大理系第3問
東大の有名な入試問題を2問ほど紹介します。上記の2つの図を知っていれば比較的簡単に解くことができます。逆に上記の図を知らないとかなりの難問です。
を一辺の長さが1の正八面体とする。
(1) の一つの面と平行な平面で を切ったときの切り口の周の長さは一定であることを示せ。
さきほど述べた断面図の性質 をきちんと説明するだけです。
(2)一辺の長さが1の正方形の穴が開いた平面がある。 をこの平面にふれることなく穴を通過させることができるか。結論と理由を述べよ。
略解:さきほどの断面図 において幅 は で高さは である。よってほんの少し回転させれば一辺の長さが の正方形にすっぽりおさまる。(周囲に触れない)
よって各高さの断面図が正方形内にすっぽりおさまるので正八面体は正方形に触れることなくを通過する。
2008年東大理系第3問
2008年東大理系第3問
同じ構図の問題が2008年にも出題されています。
(1)正八面体のひとつの面を下にして水平な台の上に置く。この八面体を真上から見た図(平面図)をかけ。
冒頭の図が解答そのものです。
(2)一辺の長さが1の正八面体の互いに平行な2つの面をとり,それぞれの面の重心を とする。 を通る直線を軸としてこの八面体を1回転させてできる立体の体積を求めよ。
回転体の軸は図の緑の点に対応します。細かい計算はやや面倒なので省略します。上記の2つの事実に加えて,断面図上で平面図形の考察が必要になります。
久しぶりの空間図形!











