正五角形の対角線の長さと作図方法

更新 2023/12/19

正五角形を（定規とコンパスのみを使って）作図する方法を解説します。

正五角形の作図の原理を理解するために，まずは1辺が1の正五角形の対角線の長さについて考えます。とにかく作図方法だけ知りたい！という方はページ下部のグレー背景部分（2箇所）のみ読んで下さい。

正五角形の対角線の長さ

正五角形の対角線

1辺の長さが1の正五角形の対角線の長さは $\dfrac{1+\sqrt{5}}{2}$ である。

正五角形

$\sqrt{5}$ は約 $2.2$ なので対角線の長さは1辺の長さの約 $\dfrac{1+2.2}{2}=1.6$ 倍です。
$1:\dfrac{1+\sqrt{5}}{2}$ は黄金比と呼ばれます。有名な値なので覚えておくとよいです。→黄金比が現れるいろいろな例（方程式・図形・数列）と現れる理由
正五角形の対角線の長さを求める方法はいくつかあります。例えば，
- トレミーの定理を用いる方法→トレミーの定理とその証明，応用例の応用2
- 三角形の相似を用いる方法→覚えておくと便利な三角比の値～18°の三角比の導出2

→高校数学の問題集　～最短で得点力を上げるために～のT136でも関連する問題と計算ミスを減らすコツを解説しています。

ここから正五角形の作図方法を解説していきます。細かい書き方の手順を1つ1つ覚えるよりも大雑把な方針を理解してください！

手順1．適当な長さの線分 $AB$ を書く

手順2． $AB$ の $\dfrac{1+\sqrt{5}}{2}$ 倍の長さの線分を作図する

手順3．正五角形 $ABCDE$ を作図する

1は当然簡単，2が出来てしまえば3も簡単です。つまり，正五角形の作図方法の最大の山場は2になります。

手順2までについて具体的な作図方法を解説します。

作図方法（手順2まで）

手順1：まず適当に線分 $AB$ を書く。

手順2−1： $AB$ の垂直二等分線 $l$ を作図する。 $AB$ と $l$ の交点（ $AB$ の中点となる）を $M$ とおく。

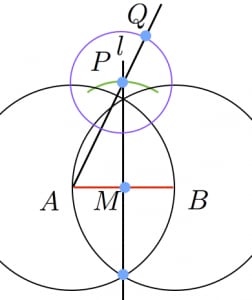
正五角形の作図

手順2−2：「中心 $M$ ，半径 $AB$ の円（緑）」と $l$ の交点を $P$ とする。すると， $AP=\sqrt{AM^2+MP^2}=\dfrac{\sqrt{5}}{2}AB$ となる。

手順2−3：「中心 $P$ ，半径が $\dfrac{AB}{2}$ である円（紫）」と直線 $AP$ の交点のうち $A$ と遠い側のものを $Q$ とする。このとき $AQ=\dfrac{1+\sqrt{5}}{2}AB$ となる。

作図のポイントは以下です：

$\phi=\dfrac{1+\sqrt{5}}{2}AB$ の長さの線分が作図できればあとは簡単です。

手順3です！

作図方法〜完結編〜

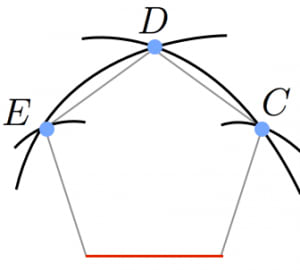
正五角形の作図2

ただし，直線 $AB$ に関して $C,D,E$ が全て同じ側に来るようにとる。すると， $ABCDE$ は正五角形となる。

当サイト初の作図にまつわる記事です。

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！