三次関数の対称性と4等分の法則

三次関数のグラフに関して以下の性質が成り立つ:
-
変曲点に関して点対称である
-
図において, は等間隔に並んでいる(4等分の法則)
( は変曲点, は極大,極小点, は極大,極小点と同じ高さの点の 軸への射影)
変曲点に関して点対称であることの証明
変曲点に関して点対称であることの証明
三次関数のグラフが変曲点に関して点対称であることは広く知られています。証明してみます。
「変曲点に関して点対称」という性質は平行移動に関して不変です。よって,変曲点を平行移動で原点に持ってきたものだけを考えればよいのです。具体的には, を平行移動して二次の係数 と定数項 を消します。
を適当に平行移動して二次の係数と定数項を消す。
つまり, という形のものだけ考えれば良い。
これが原点に関して点対称であることを示す。
がグラフ上にある
⇔
⇔
⇔ がグラフ上にある
よって,変曲点に関する点対称性が示された。
4等分の法則
4等分の法則
の場合を考えますが の場合も同様です。また,3次関数は必ず極大・極小点を持つとは限りませんが,極大・極小点を持つ場合について考えます。
それぞれの 座標を愚直に計算して求めてもよいですが,ここでは解と係数の関係と,さきほど証明した「変曲点に関して点対称」を使ってスマートに証明します。

直線 と三次関数 の交点の 座標は三次方程式
の解である。
この方程式の3つの解の和は,解と係数の関係より である。これは によらない。つまり, 交点の 座標の和 は直線によらない。
そして,変曲点を通る直線を考えるとさきほど示した点対称性より となる。
よって,極小点を通り 軸と平行な直線について考えると より は と を に内分する点。
この事実と「変曲点に関して点対称」より四等分の法則が示された。
四等分の法則は,三次関数のグラフにまつわる幅広い問題で強力な時短・検算テクニックになるので覚えておきましょう。
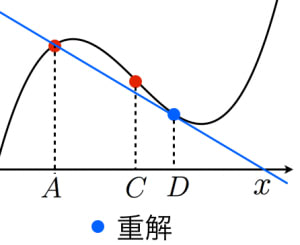
ちなみに,上記の証明から分かるように三次関数のグラフの接線が 軸と平行でない場合も, は変化しますが, は と を に内分する点です。
「四等分の法則」は一般的な用語ではありません,ご注意ください。
Tag:大学入試で頻出の有名な関数まとめ











