tanの三倍角の公式
sin と cos と同様に,tan についても三倍角の公式が成立します:
tan3θ=1−3tan2θ3tanθ−tan3θ
sin や cos とくらべて使う機会が少ないので覚える必要はありません。ただし,導出はできるようになっておきたいです。
tanの証明
tan3θ=1−3tan2θ3tanθ−tan3θ
を示す。まず,3θ=θ+2θ
と分解して,加法定理を使う:
tan3θ=tan(θ+2θ)=1−tanθtan2θtanθ+tan2θ
さらに,2θ=θ+θ と分解して,加法定理を使う:
1−tanθtan2θtanθ+tan2θ=1−tanθ1−tan2θ2tanθtanθ+1−tan2θ2tanθ=(1−tan2θ)−2tan2θtanθ(1−tan2θ)+2tanθ=1−3tan2θ3tanθ−tan3θ
余談:tan の n 倍角
tan の四倍角の公式は
tan4θ=1−6tan2θ+tan4θ4tanθ−4tan3θ
となります。二倍角・三倍角・四倍角を見比べていると,美しい規則がみつかります。
tan2θtan3θtan4θ=2C0tan0θ−2C2tan2θ2C1tanθ=3C0tan0θ−3C2tan2θ3C1tanθ−3C3tan3θ=4C0tan0θ−4C2tan2θ+4C4tan4θ4C1tanθ−4C3tan3θ
実は,帰納法を用いると
tan(2n+1)θtan(2n)θ=2n+1C0tan0θ+⋯+(−1)n2n+1C2ntan2nθ2n+1C1tanθ+⋯+(−1)n2n+1C2n+1tan2n+1θ=2nC0tan0θ+⋯+(−1)n2nC2ntan2nθ2nC1tanθ+⋯+(−1)n−12nC2n−1tan2n−1θ
が示せます。
因数分解した形(sin,cos)
三倍角の公式(因数分解した形)
sin3θ=−4sinθsin(θ+60∘)sin(θ−60∘)
cos3θ=4cosθcos(θ+60∘)cos(θ−60∘)
右辺が因数分解されており,非常におもしろいです。証明は難しくありません。右辺を加法定理で展開すれば,三倍角の公式の右辺と一致することが確認できます。
また,三倍角の公式の右辺を因数分解して合成することでも証明できます。
証明
sin3θ=−4sin3θ+3sinθ=sinθ(−4sin2θ+3)=sinθ(−sin2θ+3cos2θ)=sinθ(3cosθ+sinθ)(3cosθ−sinθ)=−4sinθsin(θ+60∘)sin(θ−60∘)cos3θ=4cos3θ−3cosθ=cosθ(4cos2θ−3)=cosθ(cos2θ−3sin2θ)=cosθ(cosθ+3sinθ)(cosθ−3sinθ)=4cosθcos(θ+60∘)cos(θ−60∘)
この公式は例えば,フランクモーリーの定理の証明に用いられます。
フランクモーリーの定理
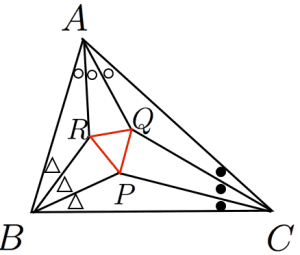
任意の三角形 ABC において,3つの角の三等分線どうしが最初にぶつかる点を
P,Q,R
とおくと,三角形
PQR
は正三角形である。
猛者は数学オリンピックの本戦対策として覚えておいてもよいでしょう。
→フランク・モーリーの定理の証明
因数分解した形(tan)
さきほどの sin と cos の式から以下の tan の式を得ます。
三倍角の公式(因数分解した形)
tan3θ=tanθtan(60∘+θ)tan(60∘−θ)
(解と係数の関係を使って tan の式を直接証明することもできます)
この公式が活躍する例題を2問紹介します。
例題1(千葉大2013)
tan10∘=tan20∘tan30∘tan40∘ を証明せよ。
解答
θ=10∘ として公式を使う:
tan30∘=tan10∘tan50∘tan70∘
これと tanθ=tan(90∘−θ)1 より目標の式を得る。
例題2(防衛医大2024)
tan60∘tan80∘tan50∘tan70∘ の値を求めよ。
解答
同じく θ=10∘ として公式を使うと,答えは 31
※この節は yama 先生に教えてもらった内容です。
Tag:三角関数の基本公式一覧

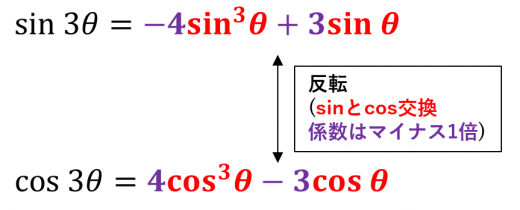 あとは,「がんばって式をそのまま丸暗記する」 または 「以下の語呂」 で と の片方を覚えましょう。
あとは,「がんばって式をそのまま丸暗記する」 または 「以下の語呂」 で と の片方を覚えましょう。











