リーマン予想の意味,素数分布との関係
更新
ゼータ関数の非自明な零点の実部は である。
自明な零点(ゼロ点)の意味,リーマン予想に関して現在分かっている基本的なこと,素数との関係,暗号との関係など解説します。
リーマン予想について
リーマン予想について
-
ミレニアム懸賞問題(一億円問題)の一つです。2023年現在,未解決です。→ミレニアム懸賞問題の概要と大雑把な説明
-
ミレニアム懸賞問題は全部で7つありますが,その中で主張の意味を理解するだけならリーマン予想が最も簡単だと思います(問題の主張を理解するのが簡単だからといって解くのが簡単とは限らない)。
リーマン予想の意味
リーマン予想の意味
リーマン予想の主張を解説します。
-
ゼータ関数 というのは 以外の複素数全体で定義された関数です。実部が より大きい複素数 に対しては という美しい式で定義されます。→ゼータ関数の定義と基本的な話
-
となる複素数 をゼータ関数の零点と言います。
-
が成立することが( 関数にある程度精通している人にとっては)簡単に分かるので負の偶数は自明な零点と呼ばれます。
以上を踏まえると,リーマン予想は
となるならば は負の偶数,または の実部が である。
と言うこともできます。
分かっていること
分かっていること
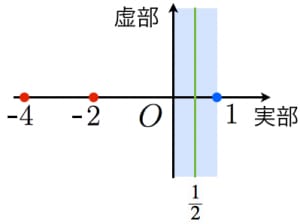
事実1:「虚部が より大きく より小さい零点」は,実部が であることが知られています。そして,そのような零点が 兆個以上あることが知られています。The Riemann hypothesis is true up to
事実2:実部が である零点が無限個存在することも証明されています(緑の直線上に零点が無限に存在する)。
事実3:非自明な零点の実部は より大きく より小さいことが証明されています(非自明な零点は青い領域にある)。
素数との関係
素数との関係
以下の素数の個数を と書きます(パイ関数)。
このとき, は が十分大きいとき で近似できます(素数定理)。→整数論の美しい定理7つ
実は,リーマン予想よりも弱い主張(上記の事実3)を認めるだけで素数定理が比較的容易に証明できます。さらに,リーマン予想が正しいとしたら素数定理の近似精度に関するよりよい理論保証が与えられます。そのような意味で リーマン予想と素数分布は関係しています。
RSA暗号との関係
RSA暗号との関係
最後に,リーマン予想と暗号の関係についてです。
RSA暗号の安全性の根拠は素因数分解の難しさです。→素因数分解の難しさと素数判定
しかし,リーマン予想が証明されたからと言って,大きな数の素因数分解が現実的な計算時間でできるようになる訳ではありません(少なくとも私の知っている&調べた限りでは)。
正:リーマン予想が証明される→素数分布の性質が( の近似精度の改善という意味で)詳しく分かる
誤:リーマン予想が証明される→RSA暗号が突破できる!
NHKスペシャル「魔性の難問 ~リーマン予想・天才たちの闘い~」という番組では上記の「誤」があたかも正しいかのような説明の仕方をしていたので残念でした。











