正多角形の作図可能性の条件
更新
正 角形が定規とコンパスで作図可能
となる 以上の整数 と互いに異なるフェルマー素数 が存在する。
定理1の主張について
定理1の主張について
フェルマー素数とは, 以上の整数 を用いて と表せる素数です。→フェルマー数とその性質
例えば, , , などはフェルマー素数です。
正三角形の作図は中学数学で習います。正五角形の作図も高校数学で理解できます。→正五角形の対角線の長さと作図方法
なんと正十七角形も作図できるのです!
正多角形が作図可能である必要十分条件
正多角形が作図可能である必要十分条件
正 角形が作図可能
長さ1の線分が与えられたときに長さ の線分が作図可能
が整数の四則演算とルートで表現できる
一つ目の について。正 角形が作図できるとき,長さの比が である2本の線分が作図できることから分かる。
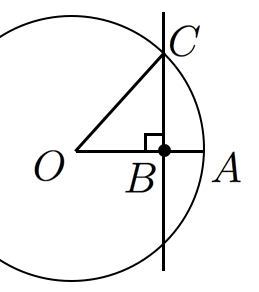
一つ目の について。長さ の線分 が与えられたときに長さ の線分 が作図できるとき, を通り と垂直な直線と中心が で半径が である円の交点の1つ が作図できる。 は正 角形の1辺である。よって,正 角形が作図できる。
二つ目の について。やや難しいので割愛。
二つ目の について。(整数の四則演算とルートで表現できる任意の数 に対して)長さ1の線分が与えられたとき,長さ の線分は作図可能。→平方根の長さを作図する2通りの方法
正十七角形の作図
正十七角形の作図
任意のフェルマー素数 に対して は整数の四則演算とルートで表現できることが知られています。証明はかなり難しいです。例えば高木貞治の「初等整数論講義」という本に載っています。
この結果とさきほどの定理2より正 角形は作図可能ということです。
ちなみに,
です。
冒頭の定理の導出
冒頭の定理の導出
(以上の事実は認めてしまった上で)冒頭の定理1の を導出します。以下の2つの事実を証明すればOKです。
-
正 角形が作図可能なら正 角形も作図可能。
-
互いに素な数 に対して正 角形と正 角形が作図可能なら正 角形も作図可能。
1について。 が整数の四則演算とルートで表現できるなら,半角の公式から も整数の四則演算とルートで表現できる。
2について。 と は互いに素なので ,つまり を満たす整数 が存在する。→一次不定方程式ax+by=cの整数解
よって,加法定理より
である。
よって, と が整数の四則演算とルートで表現できるなら, も整数の四則演算とルートで表現できる。
はかなりインパクトありますね。











