オイラーのファイ関数のイメージ
-
自然数 に対して, から までの自然数の中で と互いに素なものの数を と書き,オイラーの 関数と呼ぶことがある。
-
関数は という式で計算できる。ただし, は の素因数。
オイラーの 関数(トーシェント関数)についての話です。
オイラーのファイ関数の計算例
オイラーのファイ関数の計算例
と素因数分解できるとき, となります。この公式を使えば,「自然数 と互いに素な 以下の自然数の個数」を高速で求めることができます。
と互いに素な 以下の自然数の個数は,
より, 個。
実際に全列挙すれば, の つで正しいことが確認できる。
と互いに素な 以下の自然数の個数は,
より, 個
実際に全列挙するのは疲れるのでファイ関数の公式が役に立った。
この手の問題は入試問題でたまに出題されます。数学オリンピックの整数問題でも役に立つかもしれません。
→高校数学の問題集 ~最短で得点力を上げるために~のT67でも,類題と3通りの解答を紹介しています。
オイラーのファイ関数のイメージ
オイラーのファイ関数のイメージ
厳密な証明の前に,まずはファイ関数の公式のイメージです。
と素因数分解される場合について, から までの自然数の中で と互いに素なものがいくつあるか考えます。
「 と互いに素」⇔「 と互いに素,かつ と互いに素,かつ かつ と互いに素」という素数の性質を利用します。
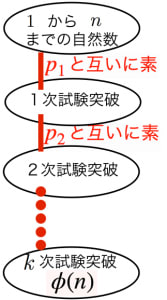
まず, から の中で と互いに素なものの割合は, 。
生き残った 個の中で と互いに素なものの割合は,
さらに生き残った 個の中で と互いに素なものの割合は,
これを繰り返すとオイラーのファイ関数の公式を得る。
の部分が厳密ではないです。
ファイ関数の公式の証明
ファイ関数の公式の証明
公式のイメージがわかったところで, を証明してみましょう。
3段階にわけて証明します。まずは,( は素数で は正の整数)と表される場合を考えます。
の場合, は 以下の正の整数で の倍数でないものの数なので となる。
次は一番難しい第2段階です。オイラーのファイ関数の乗法性を証明します。
が互いに素なとき, であることを示す。
以下の正の整数を で割ったあまりごとで 個の集合にわける。余りが である集合を とおく。 ごとに「 と互いに素」なものの数を数える。
- と が互いに素でない場合。 と の最大公約数を とおくと, に属する整数はすべて の倍数なので と互いに素なものはない。
- と が互いに素な場合。 と互いに素なものの個数は 個(なぜなら の要素はすべて と互いに素であり,さらに の要素を で割った余りはすべて異なり(→補足) から を尽くすので 個が と互いに素)。
後者のようなグループは 個あるので,結局
補足: と を で割った余りが同じと仮定すると が の倍数となり矛盾。
最後は簡単です。
と素因数分解されるとき,乗法性を繰り返し使うと
ここで右辺の各項に第一段階の結果を使うと,求めたい公式を得る。
ファイ関数の和
ファイ関数の和
が成り立つ。
とは, の全ての約数 について和を取るという意味です。例えば とすると,
となります。
とする。 と の約数 について,
と との最大公約数が が整数かつ と は互いに素 が のいずれか,かつ と は互いに素
一番最後の条件を満たす の個数は, である。
よって, の要素を との最大公約数 でグループ分けすることにより, が分かる。 が の約数 が の約数であることに注意すると目標の式を得る。
実は,この性質とメビウスの反転公式を使って冒頭の公式をきちんと証明することもできます。→メビウスの反転公式の証明と応用
オイラーの定理
オイラーの定理
ファイ関数に関連する定理として以下の「オイラーの定理」が知られています。
を自然数, を と互いに素な正の整数としたとき, となる。
が素数の場合はフェルマーの小定理になります。フェルマーの小定理の証明と例題
以上 以下で と互いに素な整数を とおく。
で割った余りで見ると, という集合は と一致する(→補足)。よって,すべて掛け算すると
ここで,各 は と互いに素なので,合同式の両辺を で割って を得る。
補足:以下の2つの主張よりわかります。
- と を で割った余りは異なる(同じだと仮定すると が の倍数になり矛盾)。
- 各 は と互いに素になる。
オイラーのファイ関数の公式は徐々にふるい落とすイメージです。
Tag:オイラーの公式・定理まとめ











