パスカルの三角形の性質とフラクタル
パスカルの三角形において,偶数を0,奇数を1と書きなおしたものを考えるとおもしろい規則性がある。
パスカルの三角形に関するおもしろい性質と,関連する入試問題を紹介します。
パスカルの三角形と偶奇
パスカルの三角形と偶奇
-
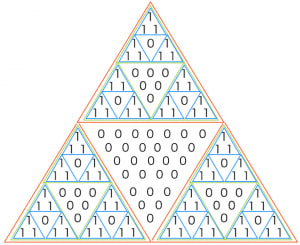
パスカルの三角形において偶数を0,奇数を1としたものは図のようになります。色のついた三角形はとりあえず無視して0と1という数字のみに注目して下さい。
-
上から 段目,左から 番目の数字が二項係数 に対応しています。例えば,上から4段目,左から2番目には「1」があるので が奇数であることを表しています。
簡単な構成法とフラクタル
簡単な構成法とフラクタル
実は上の図は美しい規則性のおかげで簡単に作ることができます!
-
最初に1段目,2段目(一番上の青い三角形の部分)を書く。
-
今作った三角形を左下と右下にコピーして二倍のサイズの三角形をつくる。
-
真ん中の空いたスペースには0を入れる。
-
以下2と3を繰り返す。
各段階で作った三角形を違う色で囲むと上図のようになります(1段階目は青,2段階目は緑,3段階目は赤)。
少し見にくいですが, 青い三角形の中は全て1,外は全て0となっています!
なお,上の構成法が正しいことは帰納法で簡単に証明できます。練習問題にどうぞ。
上記の操作を無限に繰り返していくとフラクタル構造(シェルピンスキーのギャスケットと呼ばれるもの)が現れます。
※「無限に繰り返す」という表現は厳密ではありませんが,ここではフラクタル構造っぽさ,自己相似っぽさがなんとなく分かればOKです。
上の構成法から分かる性質
上の構成法から分かる性質
-
性質1:各段階で一番下に来る行には全て1が並ぶ。つまり, が ( は非負整数)という形のとき, なる任意の に対して は奇数である。
-
性質2:逆に, が という形でないとき,ある ()が存在して は偶数である。
性質1は構成法のステップ2から,性質2は構成法のステップ3からただちに分かります。
東大の問題
東大の問題
1999年東大理系第5問です。東大の問題の中でもけっこう難しい問題だと思いますが,上記の構造を知っていると一瞬で答えが分かります。
を自然数とする。 とおくとき, を満たす全ての整数 について,二項係数 は偶数であることを示せ。
以下の条件を満たす自然数 を全て求めよ。
条件: を満たす全ての整数 について,二項係数 は奇数である。
さきほどの構成法が正しいことをきちんと書くだけの簡単な問題となります。 の答えは「 型の自然数」です。
ちなみに2015年東大理系第5問も二項係数の偶奇に関する問題でした。
を 以下の正の整数とする。 が偶数となる最小の を求めよ。
こちらについては上記の構造を知っていると「一瞬で答えが分かる」とまでは行きませんが,かなり有利になります。
さらにさらに,1991年JMO予選問9はこの記事の内容を知っていれば簡単に解けます。
シェルピンスキーのギャスケットを見るとゼルダの伝説のトライフォースを思い出します。











