全ての放物線が相似であることの証明
全ての放物線は互いに相似である。
このページでは「放物線の相似」について解説します。
そもそも,中学数学で相似を習って以来,基本的に三角形の相似ばかり扱ってきたので,「放物線が相似」と言われてもピンと来ない人が多いと思います。そこで,まずは「相似」の定義を確認します。
「相似」の2通りの意味
「相似」の2通りの意味
回転を許容するのか,許容しないのか,文脈によって使い分ける必要があります。
1.回転を許容する相似
定義1:「回転を許容する相似」とは,一方の図形が「拡大・縮小+平行移動+回転」で他方の図形に重なるという意味です。
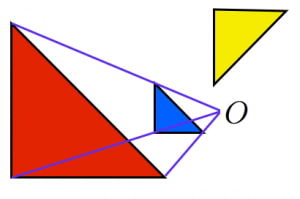
定義1では,とにかく形状が同じなら相似とみなします。図において,赤も青も黄も全部相似です。
中学数学で相似を習ったときから大学受験の問題まで,相似と言えば「回転を許容する相似」だったと思います。
「回転を許容する相似」を利用して,種々の図形問題を解いてきたのではないでしょうか。
2.回転を許容しない相似
定義2A:回転を許容しない相似とは,一方の図形が「拡大・縮小+平行移動」で他方の図形に重なるという意味です。
実は,回転を許容しない相似の定義は,相似の中心を用いた以下の定義とも同値です。
定義2B:図形 をある点 を中心に拡大(または縮小)したものが図形 になるときに と は相似であると言い,点 を相似の中心と言います。
数学オリンピックの問題などでは,ある点を中心とした相似変換を考えることで簡潔に証明できる場合もあるため,回転を許容しない相似も重要です。
さきほどの図において,赤と青は点 を相似の中心とする相似な図形ですが,黄色は相似ではありません。回転を許容しない分,より強い定義になっています。
放物線が相似であることの証明
放物線が相似であることの証明
のグラフとして表される放物線たちは,強い意味で,すなわち回転を許容しない相似です。任意の2つの放物線に対して相似の中心が存在して,一方は他方の拡大(縮小)になっています。
ただし,相似の中心を求めるのは計算がめんどうなので,ここでは2つの放物線が定義2Aを満たしていることを証明します。
2つの放物線 と が平行移動と拡大で重なることを示せばよい。そして,平行移動によって頂点を重ねることができるので, と が原点を中心とする拡大で重なることを示せば十分である。
上の点 を原点を中心に 倍に拡大すると となり,放物線 上の点にうつる。
また, が実数全体を動くとき, も実数全体を動くので,2つの放物線 と は拡大により重なることがわかった。
あとは,「方針」に記載したことより,任意の2つの放物線が相似であることが分かる。
グラフの拡大については,関数のグラフの拡大・縮小の証明と例を参照してください。
ちなみに,当たり前ですが全ての円も相似です。→接する2つの円の相似の中心
普段何気なく使う言葉でも,定義をきちんと確認し直すことは大事です。











