1のn乗根の性質と複素数平面
更新
乗して になる複素数,つまり の 乗根について,3つの性質を紹介します。
-
1の 乗根は複素数平面の単位円周上に等間隔で並ぶ。
-
1の 乗根は全部で 個あるが,それらの和は0である。
-
1の 乗根のうちどれでもよいので1つを とおくと
1の三乗根,四乗根
1の三乗根,四乗根
まずは,具体的に の場合を考えてみます。
の三乗根を計算して,3つの性質を確認せよ。
の解が の三乗根である。
- これを複素数平面上に図示すると,単位円周上に等間隔で並ぶ。

- つの三乗根の和は,
- 3つの三乗根いずれについても は簡単な計算で確認できる。
※1の三乗根については1の三乗根オメガを用いた計算と因数分解でより詳しく説明しています。
の四乗根を計算して,3つの性質を確認せよ。
の解が の四乗根である。
- これを複素数平面上に図示すると,単位円周上に等間隔で並ぶ。
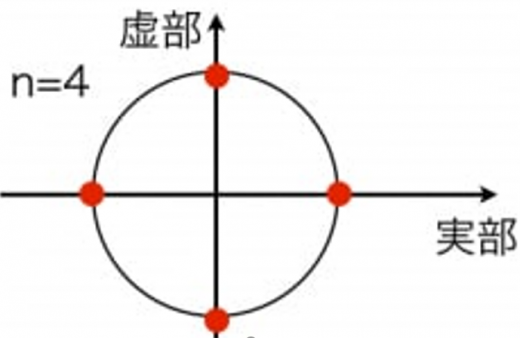
- つの四乗根の和は,
- 4つの四乗根いずれについても は簡単な計算で確認できる。
1のn乗根と単位円
1のn乗根と単位円
ここから3つの性質の証明です。
まずは,1つめです。1の 乗根は複素数平面の単位円周上に等間隔で並ぶことを証明します。
考え方はいくつかありますが,前提知識として「複素数の積と回転が対応していること」の理解が必要です。
・ の 乗根は 個以下であること
の 乗根は の解である。 次方程式の解は重複度込みで 個(代数学の基本定理)なので の 乗根は全部で 個以下である。
・実際に 乗根を構成する
たちが の 乗根であることはド・モアブルの定理を用いることで以下のように確認できる:
は単位円周上に等間隔で並ぶので,目標の性質が証明された。
なお, ( の 乗根の の場合のもの)を と書くことが多いです。
また,このように を定めると, の 乗根たちは と書けることも分かります。
1のn乗根の和
1のn乗根の和
次は2つめの性質です。1の 乗根の和が であることを証明します。解と係数の関係を使うだけです!
の 乗根たちは方程式 の解である。
よって,解と係数の関係よりそれらの和は である。
図形的に説明することもできます。
の 乗根たちは複素数平面上で正 角形の頂点たちとなる。
その正 角形の重心は対称性より原点にある。
よって, の 乗根たちの和は である。
1のn乗根の共役
1のn乗根の共役
次は3つめの性質 を証明します。右側の等号は からすぐにわかります。
性質2の証明で述べたように,1の 乗根は,ある整数 を用いて とおける。複素共役を取ると, である。一方, 乗すると,ド・モアブルの定理より ここで,三角関数の中身が となることと,, に注意すると,結局 となる。つまり
1の5乗根
1の5乗根
1の5乗根は,相反方程式とその解き方の考え方を使って具体的に計算できます。
の5乗根は, と ただし, が3つあるが,1つめと3つめは同じ符号を選ぶ。あとは任意。
を解けばよい。移行して因数分解すると, 第二因数について,相反方程式なので で割って変形すると, とおくと, つまり,
一方, を について解くと から
以上より, ただし, が3つあるが,1つめと3つめは同じ符号を選ぶ。4つの解を得られる。
1の17乗根もとても大変ですが2次方程式を繰り返し解くことで計算できます。高木貞治の初等整数論講義には「1のp乗根,特に17乗根」という章があります。











