二項定理の意味と係数を求める例題・2通りの証明
二項定理とは,
を展開したときの の係数は である
という定理。
二項定理(英:binomial theorem)は見た目が少し複雑ですが,慣れてしまえば難しくありません。二項定理の意味と,二項定理の2通りの証明を解説します。
二項定理の意味
二項定理の意味
二項定理は,
「 を展開したときの の係数は になる」
という定理です。ただし,
- とは を 回かけたものです。例えば, です。
- は「 個のものから 個選ぶ場合の数」です。二項係数と呼ばれます。→二項係数の有名公式一覧と2つの証明方針,→順列と組合せの違いと例題
を二項定理を使って展開してみる。 として二項定理を使う。
- として, の係数は
→項としては が出てくる - として, の係数は
→項としては が出てくる - として, の係数は
→項としては が出てくる - として, の係数は
→項としては が出てくる
つまり,展開した結果は
例題
例題
二項定理を用いて係数を計算する
を展開したときの の係数を計算せよ。
二項定理で とすると,
「 を展開したときの の係数は 」
となる。よって, が現れる項は の部分であり,係数は
である。
を展開したときの の係数を計算せよ。
二項定理で とすると,
を展開したときの の係数は
となる。よって, が現れる項は の部分であり,係数は
数列の和への応用
ここから少し難しいです。
を求めよ。
二項定理をうまく当てはめる:
を求めよ。
例3 の計算と同様にすると これらを足すと となる。よって
パスカルの三角形と二項係数の関係
パスカルの三角形と二項係数の関係
以下の2つの規則から作られる三角形をパスカルの三角形という。
- 最頂点の数と,各行の左右の端の数は全て
- 各行の左右の端以外は,左上の数と右上の数の和
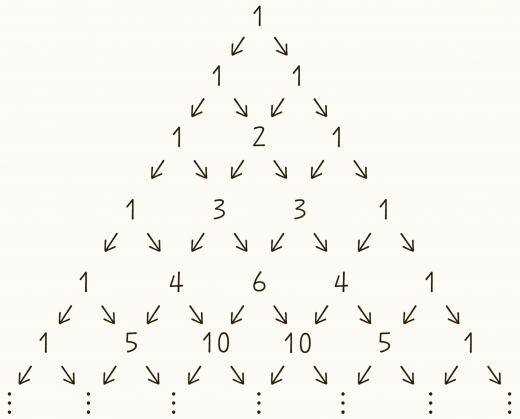
パスカルの三角形における 行目の数の並びが, の係数になっています。例えば, ですが,係数の は 行目に対応しています。
があまり大きくない時には,パスカルの三角形の図を書いて計算できます。
パスカルの三角形の面白い性質について,パスカルの三角形の性質とフラクタルの記事で解説をしています。合わせて読んでみてください。
二項定理の頻出形
二項定理の頻出形
二項定理で, としたバージョンも頻出です。つまり,
を展開したときの の係数は
です。
を展開したときの の係数を計算せよ。
答えは,
余談
ちなみに,は二項定理の特殊ケースに見えますが,こちらからもとのバージョンを導出することもできます。実際 とおいて両辺に をかけると,
となりますが,左辺は に注意して変形すると になります。
二項定理の証明1
二項定理の証明1
二項定理の証明を2つ紹介します。
まずは,教科書にも載っている定番の方法です。組合せの議論を用います。
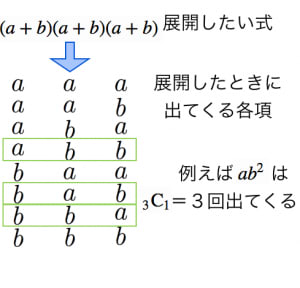
の場合を図に示す。
を展開したときに出てくる1つの項は,
「 と のうちどちらかを選ぶ」という操作を各カッコに対して行い,選んだものを全てかけあわせたもの。このようにして出てくる項を全て( 個)足し合わせると展開式が得られる。
よって,展開後は というタイプの項のみが存在し,その係数は ( 個のうちどの 個のかっこから を選ぶのかで 通り)である。
二項定理の証明2
二項定理の証明2
教科書には載っていませんが,二項定理を数学的帰納法で証明することもできます。「任意の自然数に対して〜を証明せよ」というタイプの問題で困ったら帰納法にトライです。 →数学的帰納法をわかりやすく【例題3問、応用5パターン】
-
のときは成立する。
-
のとき二項定理が成立していると仮定する。 両辺に をかける。 右辺を展開したときには というタイプの項のみが登場し,その係数は である。ここで,二項係数の公式より なので のときにも二項定理が成立することが分かった。
最後に用いた二項係数の公式は二項係数の有名公式一覧と2つの証明方針で解説しています。
2つの証明のうちどちらが分かりやすいかは人による気がしますが,ぜひ両方とも理解してください。
帰納法は泥臭い最後の手段だから推奨しないという方もいますし,帰納法が大好きな友人もいます。私は中立派です。











