2つの円の位置関係
更新
半径が異なる2つの円の位置関係は以下の5通り。
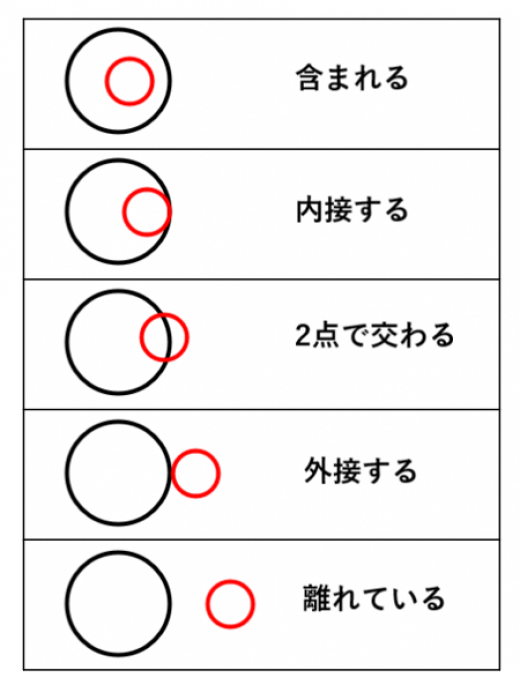
2つの円の位置関係の覚え方
2つの円の位置関係の覚え方
大きさが異なる2つの円の位置関係は5パターンあります。5パターンを丸覚えする必要はありません。小さい円を真ん中から動かしていけば,5通りが網羅できると覚えておくとよいです。
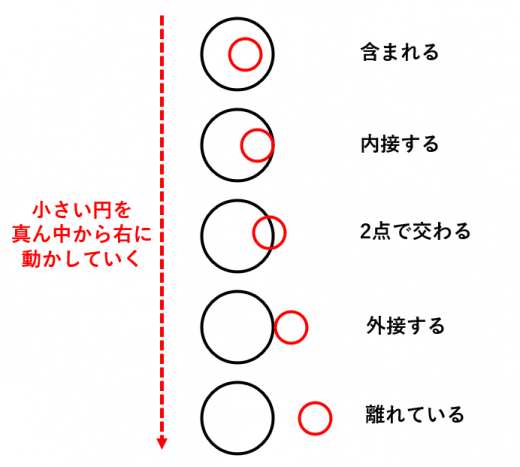 5通りの図がスラスラ描けることが重要です。
5通りの図がスラスラ描けることが重要です。
半径と中心間の距離の関係
半径と中心間の距離の関係
2つの円の半径 と中心間の距離 について,5パターンそれぞれで以下のような式が成立します。
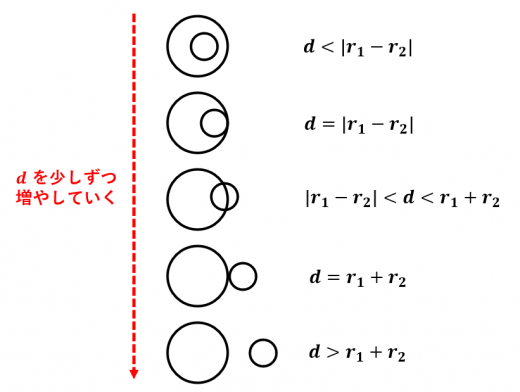
5つの式を丸暗記するのではなく,以下のように覚えるとよいでしょう。
- のときに内接する
- のときに外接する
- 上記2つが境界で, を増やしていくとパターンが変わる
2つの円 , の位置関係を求めよ。
2つの円の位置関係を求めるには がわかればよい。今回は である。また円の中心は と なので中心間の距離は である。以上より なので2つの円は外接する。
共通接線の本数
共通接線の本数
2つの円の両方ともに接する円のことを共通接線と言います。5つのパターンについて,共通接線の本数は順番に0本,1本,2本,3本,4本となります。
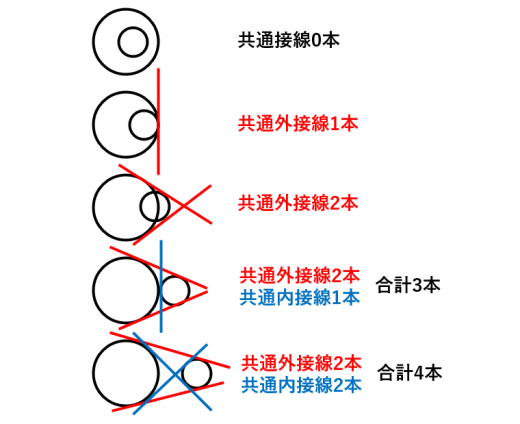
共通接線の本数は1本ずつ増えていくのがおもしろいです。
ちなみに,2つの円の交点の個数は と1ずつ変化していきます。
共通接線にまつわる発展的な話題
-
2つの円の共通内接線の交点,共通外接線の交点は相似の中心になっています(相似の中心に関しては接する2つの円の相似の中心参照)。
-
共通外接線の交点を中心とする相似の拡大比はプラスです。共通内接線の交点を中心とする相似の拡大比はマイナスです。
-
4つの円の共通外接線の長さの関係式としてケージーの定理が挙げられます。ケージーの定理はトレミーの定理の一般化で美しいです。「点は半径が無限小の円とみなす」というのが面白い考え方です。→ケージーの定理とその証明
2つの円の半径が同じ場合
2つの円の半径が同じ場合
2つの円の半径が同じ場合,2つの円の位置関係は4パターンです。「一致する」「2点で交わる」「外接する」「離れている」の4つです。
先ほどと同じように片方の円を固定してもう片方を徐々に動かしていくと4パターンになることがわかります。
参考書によっては重要かのように載っている公式ですが,丸暗記の必要はありません。











