負の二項分布の意味と期待値、分散
確率 で成功するような試行を繰り返すとき, 回成功するまでにかかる回数が従う分布は負の二項分布。
負の二項分布の意味・確率関数・期待値・分散について整理しました。
負の二項分布の意味と確率関数
負の二項分布の意味と確率関数
- 確率 で成功するような試行を繰り返すことを考えます。例えば,サイコロで「 なら成功, 以下なら失敗」という試行では です。
- 回成功するまでにかかる回数を考えます。
同様に考えると,確率 で成功するような試行を繰り返すとき, 回成功するまでに 回かかる確率は となります。
つまり,負の二項分布の確率関数は以下のようになります。
()
ただし, はパラメータです。 は を満たす実数, は整数です。
注:「 回成功するまでに何回失敗したか」が従う分布を負の二項分布と言うこともあります(むしろその方が一般的かもしれません)。その場合カウントが ずれるので注意して下さい。
他の分布との関係
他の分布との関係
-
二項分布との関係:
負の二項分布は(普通の)二項分布と状況が似ていますが,以下の違いがあります:- 二項分布 → 試行回数を固定,成功回数が確率変数
- 負の二項分布 → 成功回数を固定,試行回数が確率変数
- 二項分布 → 試行回数を固定,成功回数が確率変数
-
ガンマ分布との関係:
負の二項分布の連続バージョンがガンマ分布です。 →ガンマ分布の意味と期待値,分散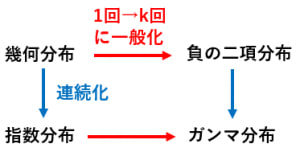
-
幾何分布との関係:
負の二項分布で としたものが幾何分布です。幾何分布は初めて成功するまでの回数が従う分布です。→幾何分布の具体例と期待値,無記憶性について
「 回成功するまでにかかる回数」=「1回成功するまでにかかる回数」+「そこからもう1回成功するまでにかかる回数」+
のように「 回成功するまでにかかる回数」 個に分解できるので,以下が成立します。
が独立に(パラメータ の)幾何分布に従うとき は(パラメータ と の)負の二項分布に従う。
負の二項分布の期待値
負の二項分布の期待値
負の二項分布の期待値は
※「 回成功するまでに何回失敗したか」の分布を負の二項分布と呼ぶ場合,期待値は になります。
証明は直接計算してもよいですが,ここでは幾何分布を利用してみます。
上記の「負の二項分布と幾何分布の関係」より,負の二項分布の期待値は,
ただし,2つめの等号は和の期待値は期待値の和【期待値の線形性】を使いました。3つめの等号は幾何分布の期待値が であることを使いました。
負の二項分布の分散
負の二項分布の分散
負の二項分布の分散は
期待値と同様に,負の二項分布の分散は,
ただし,2つめの等号では, が独立なので和の分散が分散の和になることを用いました。3つめの等号は幾何分布の分散が であることを使いました。
記事にしたい確率分布はまだいくつかあります!











