接する2つの円の相似の中心
任意の円は相似である。
特に,接する2つの円の相似の中心は接点である。
特に,2つの円が内接する場合が数学オリンピックで頻出の構図です。
相似,相似の中心の意味があいまいな人は全ての放物線が相似であることの証明参照。
接点が相似の中心であることの証明
接点が相似の中心であることの証明
全ての円が平行移動と拡大・縮小で重なるのは自明なので,接する2つの円の相似の中心が接点であることを証明します。
接点を原点として2つの円の中心が 軸上にあるように座標を設定して考えます。
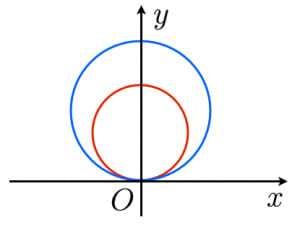
2つの円 , の相似の中心が原点であることを示せば良い。
円 上の点 は と表せる。原点を中心に を 倍に拡大すると, となり,円 上の点に移る。
また, が円 上全体を動くとき は 上全体を動くので原点(接点)が相似の中心であることが示された。
図では の場合を示しています。 と が同符号のときは内接する2つの円を表し,異符号のときは外接する2つの円を表しています。よって,拡大の比率 は,内接の場合正で外接の場合負であることが分かります。
次に,実際にこの定理が役に立つ例を見てみましょう。
数学オリンピック頻出の構図
数学オリンピック頻出の構図
円 上に3点 があり,別の円 が線分 と点 で接し,円 と点 で接するとき,
と弧 の交点 は弧 の中点
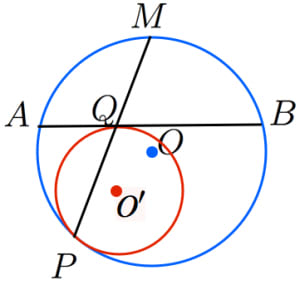
接点が2つの円の相似の中心であることを用いてこの定理を証明します!
2つの円は点 を相似の中心とする相似な図形である。 , はそれぞれ同一直線上にあるので と , と はそれぞれ対応する点である。よって と は平行である。
よって,直線 は を通り と垂直なので, は弧 の中点である。
最後に,この構図が出題された例を紹介します。
2002年日本数学オリンピック本選第一問
2002年日本数学オリンピック本選第一問
円 周上に相異なる三点 があり, が成り立っている。直線 に関して と反対側の弧 上に点 を取る。円 に点 で内接し,弦 に点 で接するとする。このとき,「点 の取り方によらず が一定である」ことを示せ。
さきほどの定理により は同一直線上にあることが分かります。線分の長さの積を評価したいときは多くの場合,相似な三角形を利用します。(方べきの定理も三角形の相似を用いて導かれます)
さきほどの定理より は一直線上にある。
と円周角の定理より,
よって,三角形 と は相似であり, =一定となる。
この構図の応用例としては他にもケージーの定理の証明があります。→ケージーの定理とその証明
よく出題される構図は覚えてしまいましょう











