モンティ・ホール問題とその解説

モンティ・ホール問題を議論するときには正解の扉の後ろには「景品」があり，不正解の扉の後ろには「ヤギ」がいるのが通例ですが，ここでは「正解の扉」「不正解の扉」という言葉を使います。

上記の解答にすぐ納得できる人は問題ないのですが（そのような人にとってはモンティ・ホール問題や，この記事はつまらないかもしれません。しかし，多くの人が陥る誤った考えを知るのも悪くはないと思います），多くの人が以下のように誤った答えを出してしまいます。

実は，私も最初は「誤った解答」が正しいと思い込んで「解答」を聞いても，なかなか納得できませんでした。じっくり考えて納得できたので「誤った直感」を正すための三つの方法を紹介します。

方法1：表をきちんと書いてみる

扉を $A,B,C$ とします。挑戦者が最初に $A$ を選ぶとしても一般性を失いません。このとき考えられるパターンは全部で四通りです。

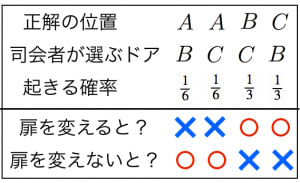
例えば一列目は「正解が $A$ であり司会者が $B$ を選ぶような確率が $\dfrac{1}{6}$ で，そのとき扉を変えると不正解，扉を変えないと正解」であることを表しています。

この表より，

扉を変えたとき正解する確率： $\dfrac{1}{3}+\dfrac{1}{3}=\dfrac{2}{3}$

扉を変えないとき正解する確率： $\dfrac{1}{6}+\dfrac{1}{6}=\dfrac{1}{3}$

となることが納得できます。

方法2：扉を100個にしてみる

扉の数を三つではなく100個に増やすと直感的に納得できる人も多いようです。

2の部分で「司会者が挑戦者に情報を与えている」というのがポイントです。これはもとの問題とは別の問題ですが，こちらの場合で納得できればもとの問題でも納得できるはずです。

方法3：プログラミングで実験してみる

乱数を使って実際にモンティ・ホール問題を何回も試行してみると，

扉を変えない場合に正解する確率→ほぼ $\dfrac{1}{3}$

扉を変えた場合に正解する確率→ほぼ $\dfrac{2}{3}$

という結果が得られます。

Tag:難しめの数学雑学・ネタまとめ