合同式(mod)の意味とよく使う6つの性質
合同式とは,わり算の余りのみに着目した等式のこと。
合同式について,意味・性質・何の役に立つのか,などを整理しました。これを読めば数学における「mod」という記号の意味がわかります。
合同式(mod)とは
合同式(mod)とは
合同式とは,大雑把に言うと割り算の余りのみに注目した等式のことです。
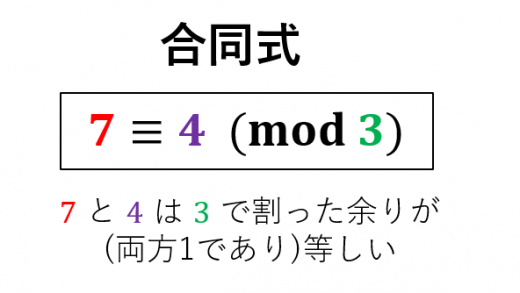
例えば, と はどちらも で割った余りが です。これを,合同式では
と書きます。
上の合同式は「7合同4モッド3」と読みます。 と は で割った余りのみに注目すれば同じという意味です。
より一般に, と を で割った余りが等しいとき,合同式では
と書きます。なお,「 と を で割った余りが等しいとき」という条件は「 が の倍数のとき」と言い換えることもできます。
mod についての補足
- 上記の のことを「法」と呼びます。
- と mod はセットで使われます。
- ただし,法 が文脈から明らかな場合は という表記を省略する場合があります。
- mod の由来は「測り」を表す「modulo(modulus の活用形)」という単語です。
合同式のよく使う性質
合同式のよく使う性質
よく使う合同式の性質を6つ紹介します。特に4,5,6が重要です。以下では明示しない限り を省略します。
1. 合同式の和
のとき,
が成立します。つまり,合同式は辺々足し算できます。
例えば, では
, なので,辺々足し算して
が成立します。
2. 合同式の差
のとき,
が成立します。つまり,合同式は辺々引き算できます。
3. 合同式の積
のとき,
が成立します。つまり,合同式は辺々かけ算できます。
特に, です。
4. 合同式の商
で, と が互いに素なら が成立します。合同式の両辺を で割って良いのは, と が互いに素である場合のみです。
合同式において,足し算,引き算,かけ算は普通の等式と同様に行ってOKですが,割り算は と が互いに素という条件がつきます(超重要)。
証明は互いに素の意味と関連する三つの定理の定理2を参照して下さい。
5. 合同式のべき乗
のとき,
を で割った余りを求めたい! しかし, を計算するのは大変。そこで なので,合同式の上の性質を使うと
と簡単に求まる。
合同式の性質5の証明は,二項定理を用いてもよいですし, の因数分解により証明することもできます。 →因数分解公式(n乗の差,和)
6. 合同式の多項式
で, を整数係数多項式とするとき,
これは,合同式の性質1,3,5を組み合わせることで証明できます。
合同式(mod)を使うメリット
合同式(mod)を使うメリット
表記簡略化による本質的な嬉しさ
「
と
を
で割った余りは等しい」と書くよりも
「」と書く方が楽です。
ほとんど差がないように感じますが,記述式で複雑な問題になると上記のような文言を大量に書く必要があるため,かなり差が出ます。また,繰り返しですが,法 が明らかなときは最初に宣言した上で を省略して書くこともできます。
余計な情報が削ぎ落とされスッキリ表現されていることで,思考の助けとなります。このように,数学における「表記簡略化」は一見表面上の意味しかないように思われますが,「思考の助けになる」という意味でとても重要です。
実際に,多くの整数問題の定理や性質は合同式を用いることでスッキリとした形で書くことができます。
が素数で が と互いに素なとき →フェルマーの小定理の証明と例題
この性質を合同式なしで書いたらめんどくさいだけでなくて,ごちゃごちゃしていて何言ってるかよく分からないという状況に直面します。
というわけで,合同式の恩恵を最大限受けるために,よく使う性質を覚えてしまいましょう!
合同式を使うさらに難しい話題
合同式を使うさらに難しい話題











