マルコフ連鎖の基本とコルモゴロフ方程式
マルコフ連鎖とは,大雑把に言うと時刻 の状態が,時刻 の状態のみに依存する(時刻 以前の状態には依存しない)ようなモデルのことです。
この記事では,確率過程の基本的な話題の1つである,マルコフ連鎖について紹介します。
マルコフ連鎖とは
マルコフ連鎖とは
マルコフ連鎖とは,
を満たすような確率変数の列 のこと。
上の式は, が のみに依存する( 以前には依存しない)ことを表しています。
例えば, 日目の天気を とし,以下の2つが成立するとしましょう。
-
によって の傾向が決まる
(例. 今日晴れたら明日も晴れやすい) -
以前は に影響しない
(2日前の天気は関係ない)
このとき, はマルコフ連鎖になります。
マルコフ連鎖の用語
マルコフ連鎖の用語
マルコフ連鎖に関する基本的な用語を整理しました。
がとりうる値の集合のことを状態空間と言うことがあります。例えば,天気の例だと状態空間は 晴れ,曇,雨 と考えることができます。晴れ,曇,雨の各状態をそれぞれ で表すと便利です。このとき と書けます。
また, のことを 遷移確率(推移確率)と言うことがあります。例えば「今日曇りだと確率 で明日晴れになる」場合,遷移確率は となります。
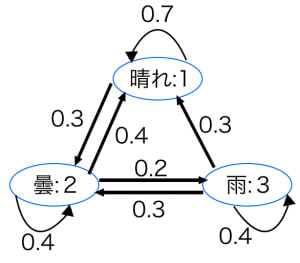
また,状態空間を頂点で表し,遷移確率を枝で表した図のようなグラフを状態遷移図と言うことがあります。確率はかなり適当ですがマルコフ連鎖の理解には役立ちます。
注:この記事では時間的に均一(遷移確率が時刻によらない)なマルコフ連鎖を考えています。
マルコフ連鎖の推移確率行列
マルコフ連鎖の推移確率行列
マルコフ連鎖において,遷移確率を並べた行列を考えてみましょう。
すなわち, 成分に「 から に遷移する確率」を入れたものを推移確率行列(または遷移確率行列,遷移行列)と言います。例えば,上のマルコフ連鎖の例では推移確率行列 は以下のようになります:
確率が満たすべき性質より,以下が分かります:
- 推移確率行列の各要素は 以上 以下である。
- 推移確率行列のどの行も,行和は である。
チャップマン–コルモゴロフ方程式
チャップマン–コルモゴロフ方程式
マルコフ連鎖の推移確率行列について「推移確率行列の 乗」と「 回の遷移の確率」が対応するという性質が成り立ちます。
推移確率行列の二乗 を計算してみると,
これは「今日の天気が分かったときに,二日後の天気がどうなるか」の確率を表します。例えば,今日晴れたら二日後晴れる確率は です。
同様に, 日後の天気の確率を求めたいときは を計算すればよいです。
もう少しきちんと書いてみます。 時刻経過に対する推移確率行列を と書くことにします。つまり, を 成分に持つ行列を とします。
すると, が成立します(右辺は推移確率行列の 乗)。
について,定義より
について考える。時刻 での状態で場合分けして への遷移確率を計算する。 の 成分を と書く。
の 成分
の 成分
以降も同様に証明できる。
上記の定理より, が成立します( 時刻ぶんの遷移の様子 と 時刻ぶんの遷移の様子 が分かれば 時刻ぶんの遷移の様子 も分かる)。この等式をチャップマン–コルモゴロフ方程式と言います。
マルコフ連鎖とマルコフ過程
マルコフ連鎖とマルコフ過程
この記事ではマルコフ連鎖について紹介しましたが,一般に,未来の状態(の確率)が過去の状態によらず現在の状態のみで決まるような確率過程のことをマルコフ過程と言います。
特に,確率変数がとりうる値の集合(状態空間)が離散的なマルコフ過程のことをマルコフ連鎖と言います。
マルコフ連鎖で記述できる入試問題もけっこうあります(特に行列が範囲内だった時代)。
Tag:数学的モデリングまとめ











