シュタイナーの内接楕円,Mardenの定理,Gauss--Lucasの定理
更新
平面図形,複素数平面における美しい定理を3つ紹介します。
シュタイナーの内接楕円
シュタイナーの内接楕円
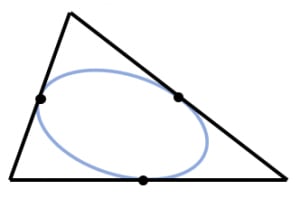
任意の三角形に対して,各辺と中点で接する楕円がただ一つ存在する。これをシュタイナーの(内接)楕円と呼ぶ。
楕円の自由度が (平行移動2,短軸の長さ,長軸の長さ,回転)であるのに対して「各辺と中点で接する」というのは つの制約になります。そう考えると,このような楕円が存在するのは少し不思議です。
さらに,シュタイナーの内接楕円の中心はもとの三角形の重心と一致します。
このような楕円が存在することは後述する Marden の定理から分かります。
Marden の定理(マーデンの定理)
Marden の定理(マーデンの定理)
Van den Berg の定理(ヴァン・デン・ベルクの定理)と呼ばれることもあります。
三次多項式 について考える。複素数平面上で の解に対応する3点 が三角形をなすとする。また, の解に対応する点を とする。このとき, を焦点とする楕円で,三角形 の各辺と中点で接するものが存在する。
まさにシュタイナーの内接楕円です。
各辺の中点を とする。
頑張って計算することにより,
が分かる(→補足)。

1より, を焦点とし を通る楕円 は, と で接する。さらに,2より, は と を通る。
さらに対称性と1より, , も成立するので, は と で と接することが分かる。
補足:この証明(の概略)はシュタイナー楕円(Aozora Gakuen)を参考にしています。詳しい計算はリンク先を参照してください。
ちなみに,後述の Gauss–Lucas の定理を使うと, が三角形 の内部(境界含む)にあることはすぐに分かります。
Gauss–Lucas の定理(ガウス・ルーカスの定理)
Gauss–Lucas の定理(ガウス・ルーカスの定理)
複素数平面において多項式 の解に対応する点を とする。 の解に対応する点は たちの凸包に含まれる。

例えば, が6次多項式のとき, の解に対応する点は(重複も含めて) つあります。図のようになったとします。すると, の解に対応する点(重複も含めて つある)は,全て図の四角形の中(境界含む)にあるというわけです。
とする。複素数 に対応する点が である。
のとき, に対応する点が の凸包に含まれることを示す。
もし, のときは は のいずれかと一致するので定理は成立。よって,以下 とする。
積の微分公式(→ライプニッツの公式の証明と二項定理)を用いて を微分すると,
よって, なので,
分母を実数化して両辺の共役複素数を取ることにより,
よって, とおくと,
と凸結合の形で書けるので定理は成立。
Marden の定理は読者の方に Twitter で教えてもらったものです。面白いです!











