最小二乗法とは，データの組 $(x_i,y_i)$ が多数与えられたときに，$x$ と $y$ の関係を表すもっともらしい関数 $y=f(x)$ を求める方法です。
この記事では，最も基本的な例（平面における直線フィッティング）を使って，最小二乗法の考え方を解説します。
最小二乗法とは
- 二つセットのデータの組 $(x_i,y_i)$ が $n$ 個与えられた状況を考えています。そして $x_i$ と $y_i$ に直線的な関係があると推察できるときに，ある意味で最も相応しい直線を引くのが最小二乗法です。
- 例えば $i$ 番目の人の数学の点数が $x_i$ で物理の点数が $y_i$ という設定です。数学の点数が高いほど物理の点数が高そうなので関係がありそうです。直線的な関係を仮定すれば最小二乗法が使えます。
最小二乗法による直線の式
まずは，最小二乗法を適用した結果を述べます。
データ $(x_i,y_i)$ が $n$ 組与えられたときに，もっともらしい直線を以下の式で得ることができます！
傾き：$A=\dfrac{\mathrm{Cov}(X,Y)}{\sigma_X^2}$
切片：$B=\mu_Y-A\mu_X$
ただし，
$\mu_X,\sigma_X$ は $x_i$ たちの平均と標準偏差。
$\mu_Y$ は $y_i$ たちの平均。
$\mathrm{Cov}(X,Y)$ は共分散です。
以下では，
最小二乗法の計算例（実データでの直線の計算方法）
最小二乗法の導出（なぜ直線の式が上のように求まるのか）
についてそれぞれ説明します。
最小二乗法による直線の計算例
最小二乗法の例として，データの数が3つの場合（普通はもっとたくさんデータがありますが）にもっともらしい直線を求めてみます。
前提知識：
分散の意味と二通りの計算方法
共分散の意味と簡単な求め方
例題
$(2,3),\:(4,7),\:(9,11)$ というデータの組に対して最小二乗法を適用してもっともらしい直線を引け。
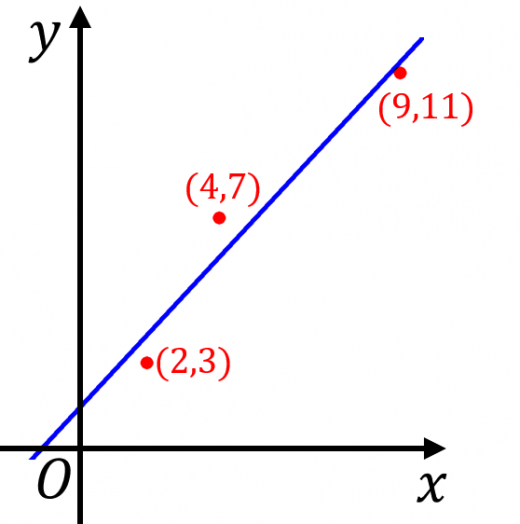
公式に当てはめて傾きと切片を求める。ひたすらに計算するのみ。
平均と分散は，
$\mu_X=5,\mu_Y=7,\sigma_X^2=\dfrac{26}{3}$
共分散は，
$\mathrm{Cov}(X,Y)=E[XY]-\mu_X\mu_Y=\dfrac{133}{3}-35=\dfrac{28}{3}$
よって，傾き：$A=\dfrac{\mathrm{Cov}(X,Y)}{\sigma_X^2}=\dfrac{14}{13}$
切片：$B=\mu_Y-A\mu_X=7-\dfrac{14}{13}\cdot 5=\dfrac{21}{13}$
よって，求める直線の方程式は $y=\dfrac{14}{13}x+\dfrac{21}{13}$
確かに $(2,3)$ や $(4,7),(9,11)$ は全てこの直線に近い点になっています。
最小二乗法の考え方（直線の式の導出）
直線フィッティングの複雑な式を導出します。考え方は非常に単純です。
もっともらしい直線の式を $y=Ax+B$ とおくと，$(x_i,y_i)$ とその直線との $y$ 方向の誤差（ズレ）は，$|y_i-Ax_i-B|$ です。この誤差の二乗和が最小になるのが最もらしい直線であると考えるのが最小二乗法の流儀です。
つまり，$\sum (y_i-Ax_i-B)^2$ を最小化するような $A,\:B$ を求める問題となりました。変数が $A,B$ でそれ以外は定数である（データによって与えられている）ことに注意して下さい。
これは，二変数の二次関数で紹介したいずれの手法で解くこともできます。数式がやや複雑ですが頑張って計算すると冒頭の直線フィッティングの式を得ます。
偏微分の方法でやってみます（読みとばしても構いません）。
証明の概略
$\sum(y_i-Ax_i-B)^2\\
=A^2\sum x_i^2+nB^2+\sum y_i^2\\
\:-2A\sum x_iy_i-2B\sum y_i+2AB\sum x_i$
$A$ で偏微分：$2A\sum x_i^2-2\sum x_iy_i+2B\sum x_i=0$
$B$ で偏微分：$2nB-2\sum y_i+2A\sum x_i=0$
これは $A$ と $B$ に関する二元一次連立方程式なので解ける。頑張って解いて計算すると冒頭の式を得る。
面白い性質
最小二乗法による直線の式
傾き：$A=\dfrac{\mathrm{Cov}(X,Y)}{\sigma_X^2}$
切片：$B=\mu_Y-A\mu_X$
から，以下の性質が分かります。
- $A\mu_X+B=\mu_Y$ より，最小二乗法による直線は $(\mu_X,\mu_Y)$ を通ります。
- 共分散が正 $\iff$ 最小二乗法による直線の傾きが正であることが分かります。これにて「無相関なら（相関係数が $0$ なら）直線的な関係がない」という説明が数学的にきちんとできたことになります。
→独立と無相関の意味と違いについて
最小二乗法の応用
- 物理実験でも最小二乗法は登場します。例えばあるバネのバネ定数を測りたいとき，フックの法則 $F=kx$ という直線的な関係があるので以下のように考えることができます：
$x$ と $F$ の組をいくつか測ってプロットする。最小二乗法で直線を引いてその傾きが $k$ である。 - 最小二乗法を行列を用いて定式化することもできます。→最小二乗法の行列表現（単回帰，多変数，多項式）
Tag: 数学的モデリングまとめ（回帰分析）