正三角形の面積,正四面体の体積を求める公式
(i)1辺の長さが の正三角形の面積 は,
(ii)1辺の長さが の正四面体の体積 は,
記述式の場合途中経過を求められるので,この公式を用いることはできませんが,検算に用いることはできます。特に,(ii)はその場で計算しようとするとわりと時間がかかってしまうので,公式の出し方まで含めて覚えておくべきです。
正四面体の体積は「底面積×高さ× 」を普通に計算すれば導出できますが,ここではサラスの公式を用いて(ii)のエレガントな導出を紹介します。
正三角形の面積公式の求め方
正三角形の面積公式の求め方
ここでは2通りの方法で正三角形の面積公式を求めてみましょう。
求め方1 〜底辺×高さ÷2を使う〜
下図のように正三角形 について角 の二等分線を引いてみます。

すると, は の中点になるので, です。
よって,三平方の定理より,
三角形の面積は底辺×高さ÷2でしたから,求める面積 は,
となります。
求め方2 〜sinを用いた三角形の面積公式を使う〜
高校で習うsinを用いた三角形の面積公式を使うことでも,公式を導出できます。一般の三角形 の面積 は,公式により
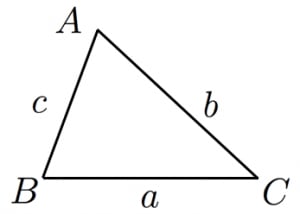
と表されます。この公式については,sinを用いた三角形の面積公式 をご覧ください。
いま, が正三角形の場合は
であるから,公式にしたがい,求める面積 は,
となります。
サラスの公式を用いた正四面体の体積の導出
サラスの公式を用いた正四面体の体積の導出
正四面体はうまく座標空間にはめこむことができます。ちなみに,正二十面体も座標空間にはめこむことができます。 →正二十面体の対角線・体積・内接球などを座標で計算

座標空間上に一辺 の正四面体 を以下のように構成する:
, , ,
原点を1つの頂点として座標軸に平行な一辺の長さが2の立方体をイメージすれば分かりやすいだろう(図参照)。
四面体 の体積はサラスの公式より以下のように求まる。
ここで,正四面体の体積は1辺の長さ の3乗に比例するので,
と書けることに注意すると, となり(ii)を得る。
非常にお世話になる機会が多い公式の1つです
Tag:三角形の面積を求める公式まとめ











