極大値・極小値の意味と求め方

- 極大(きょくだい)とは,近所で一番大きいことを表す。
- 最大とは,全体で一番大きいことを表す。
極大・極小について,意味・例題・注意点などをわかりやすく解説します。
極大・極小とは
極大・極小とは
-
極大とは,自分の近くの範囲で一番大きいという意味です。
-
もう少しきちんと言うと,以下のようになります。
ある正の実数 が存在して なら 」が成立するとき, を極大値と言う。
が の近所では, が最大という意味です。

-
極小値も同様です。極小とは,自分の近くの範囲で一番小さいという意味です。
-
また,極小値,極大値を合わせて極値と言います。
極値の求め方と例題(三次関数)
極値の求め方と例題(三次関数)
関数 が微分可能な場合,以下が成立します。
- 極大・極小の点では となる。
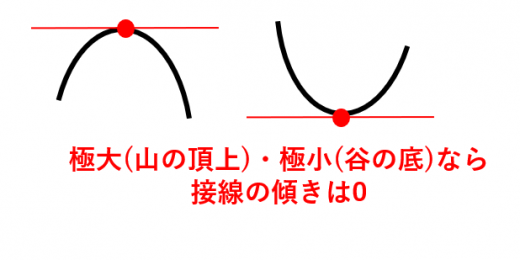
- さらに, がプラスからマイナスに切り替わる点が極大。
 微分係数 は接線の傾きです。これがプラスからマイナスに切り替わるのが山の頂上(極大)というわけです。
微分係数 は接線の傾きです。これがプラスからマイナスに切り替わるのが山の頂上(極大)というわけです。 - 逆に, がマイナスからプラスに切り替わる点が極小。
以上の性質をふまえると,以下の手順で極大・極小の点を求めることができます。
- を解く。その解が極値の候補。
- その候補の前後で の符号が変化するか確認する。プラスからマイナスに変化すれば極大。マイナスからプラスに変化すれば極小。
実際に極値を求めてみましょう。
の極値を求めよ。
微分すると,
を解くために因数分解すると,
よって, の解は となる。これが極値を取る点の候補。
- の前後では微分係数が+から−に変わるので極大。極大値は
- の前後では微分係数が−から+に変わるので極小。極小値は
微分可能な場合の極値の条件
微分可能な場合の極値の条件
極値の性質とその証明を整理しておきます。
一部はさきほどの例題でも述べましたが, が微分可能な場合には,以下の性質1~3が成立します。
が で極大または極小
-
説明その1
山の頂上では接線の傾きは なので,極大なら 。極小も同様。 -
説明その2
の十分近くでは と一次近似できる(一次近似の意味とよく使う近似公式一覧)。また, で極大なら十分小さい に対して つまり かつ
よって かつ つまり
性質1の逆は成立するとは限らない。つまり, でも で極大または極小とは限らない。
という関数を考える。
, である。しかし, は極大値でも極小値でもない( では , では )。
- が正から負に切り替わるなら極大点
- が負から正に切り替わるなら極小点
接線の傾きが正から負に変わる 上り坂から下り坂に変わる 極大点
といえる。また,性質1の説明その2と同じく一次近似の考え方からも説明できる。
なお,多変数関数の場合はややこしくなります。→多変数関数の極値判定とヘッセ行列
極大と最大の違い
極大と最大の違い
-
極大(極小)は「自分の近くの範囲で一番大きい(小さい)」という意味でした。
最大(最小)とは「全体の中で一番大きい(小さい)」という意味です。 -
最大(世界で一番大きい)なら極大(近所でも一番大きい)ですが,逆は成り立つとは限りません。

-
紫の点は「極大」であり「最大」です。
赤い点は「極大」ですが「最大ではない」です。 -
極大(極小)は自分の周りだけで決まる局所的な性質です。最大(最小)は全体で決まる大域的な性質です。
ちなみに,最大をきちんと定義すると定義域内の任意の実数 に対して のとき, を最大値と言うです。
微分不可能な場合の極大・極小
微分不可能な場合の極大・極小
「微分が−から+に変わるところが極小」という覚え方をしている人がいますが,それは微分可能な場合の話です。一般的な定義だと思ってはいけません。例えば極端な例ですが,図のような関数は の前後で微分が−から+に変わりますが極大です。
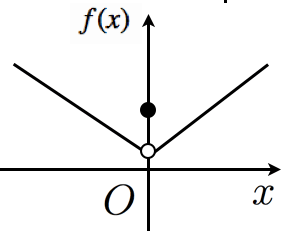
微分は一次近似である,ということを教科書でもう少し強調して欲しいですね。











