格子点の個数を数える問題の5通りの解法
座標平面において,各成分が全て整数である点を格子点(こうしてん)と呼ぶ。
例えば などは格子点です。
格子点の個数を数える問題
格子点の個数を数える問題
「特定の領域に含まれる格子点の数」を数える問題は頻出です。
まずは簡単な例を見てみましょう。
内の格子点の数を求めよ。
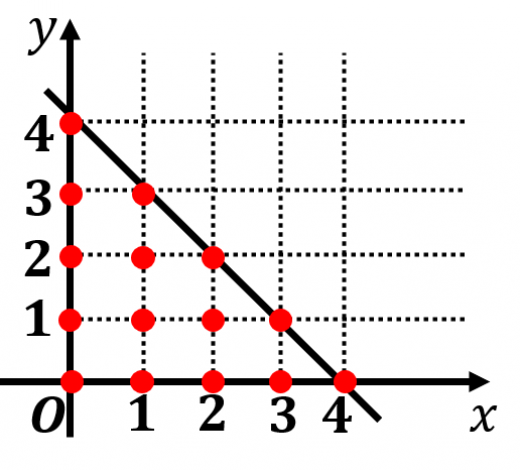
上の格子点の数は5個
上の格子点の数は4個
上の格子点の数は3個
上の格子点の数は2個
上の格子点の数は1個
よって,全部で 個
このように, の値で場合分けして数えると数えやすいです。
次は難しい問題です。2008年名古屋大学の問題を考えます。
を満たす 以上の整数の組 の個数を求めよ。
同じく, の値で場合分けして考えましょう。
と固定した部分で領域内にある格子点の数 は,
つまり
を満たす整数
の数と等しい。

- が偶数のとき, から までの整数なので,
個(→補足) - が奇数のとき, から までの整数なので,
個
よって,求める格子点の数は
補足: から までの整数の個数は の4個です。3個ではありません。同様に, から までの整数の個数は 個になります。
yを固定して考える
yを固定して考える
さきほどは の値で場合分けして数えましたが, の値で場合分けして数えることもできます。

上の格子点の数は5個
上の格子点の数は4個
上の格子点の数は3個
上の格子点の数は2個
上の格子点の数は1個
よって,全部で 個
例題1の場合は, で場合分けしても で場合分けしても実質同じでした。
例題2の場合は, で場合分けすると計算が少しめんどうになります。分母に3が登場してしまうからです。
例題2を を固定して計算してみよう。
斜めに切る
斜めに切る
「斜めに切る」ことで格子点を数えることもできます。計算がめんどうになるのであまり使いませんが,一応紹介しておきます。

上の格子点の数は5個
上の格子点の数は4個
上の格子点の数は3個
上の格子点の数は2個
上の格子点の数は1個
例題2を を固定して計算してみよう。
長方形の半分とみなす
長方形の半分とみなす
「長方形領域なら格子点の数は簡単に数えられる」ことを使って解いてみましょう。対角線部分に注意する必要があります。
図の大きな正方形には 個の格子点がある。
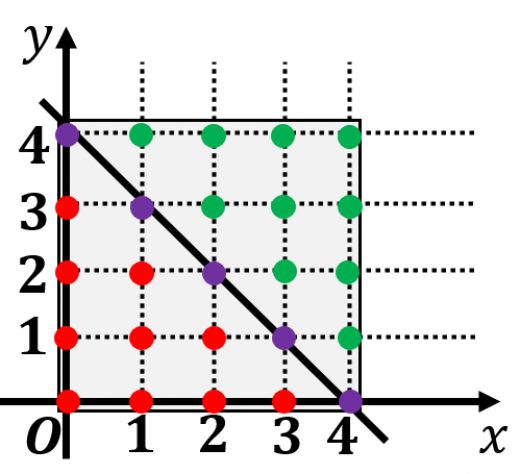
- 赤と緑は同じ数
- 対角線上の紫は5個
よって,赤+紫+緑=25 より 赤は 個
よって,求める格子点の数は,赤+紫=15
を満たす 以上の整数の組 の個数を求めよ。

-
と を結ぶ線分を対角線とする長方形上(周も含む)にある格子点の数は,
-
線分 上にある格子点の数は, 以上 以下の偶数の数と等しいので
よって,数えたい格子点のうち, を満たす格子点の数は,
「対角線上にない格子点の数」+ 「対角線上にある格子点の数」
最後に 上にある格子点の数( 個)と 上にある格子点の数( 個)を足し合わせると,
ピックの定理を使う方法
ピックの定理を使う方法
格子点の数を数える裏技としてピックの定理があります。
頂点がすべて格子点である多角形について,
が成立する。ただし は面積, は辺上にある格子点の数, は内部にある格子点の数。
, はすぐにわかる。
よってピックの定理より,
よって求める格子点の数は
ピックの定理は領域の各頂点が格子点でないと使えません。(今回は が頂点になっている)。それでも強引に使おうとすると「領域を二つに分割して,大きい方をピックの定理で求めて,小さい方は直接数える」という方法になります。
で分割する or で分割する,いずれにせよ計算はそんなに楽にはなりません。やってみてください。
読み方は「かくしてん」ではなく「こうしてん」です。











