有名不等式logx≦x-1の証明と入試問題
任意の正の実数 に対して
対数を1次関数で近似したいときに使える有名不等式です。入試でも頻出です。
logx≦x-1の証明
logx≦x-1の証明
定石通り両辺の差を微分するだけで証明できます。簡単です。
とおく。
より は で減少, で増加関数なので で最小値を取る。
これと より目標の不等式は示された。
この不等式に関して
この不等式に関して
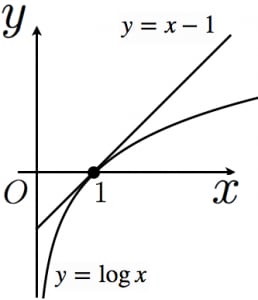
- の における接線が であることに注意して図を描くと,直感的には明らかな不等式です。
- 対数関数を上から簡単な関数(1次関数)で押さえたいことがしばしばあります。そのようなときに威力を発揮する不等式です。入試問題でももちろんですが,大学に入ってからも活躍する不等式です。
- と置換すると は となり指数関数の有名不等式と一致します。→マクローリン型不等式(指数関数) つまり,本質的には と同じなのですが,使用頻度が高いので対数バージョンでも覚えておくとよいでしょう。
- 入試で出題されるときはたいてい誘導がついていますが,この不等式を使うときは証明も添えるようにしましょう。
有名な入試問題
有名な入試問題
どこの大学か覚えていませんが,複数回見た記憶がある入試問題です。実は応用上も重要な意味を持つ問題です。
追記:読者の方に「1997年の京都府立医大で出題された」と教えていただきました。
正の実数
が を満たすときに以下の不等式を証明せよ:
対数を上からおさえる不等式を持っているので,小さい側に対数を寄せ集めます。
なので示すべき不等式は以下と同値:
これを目指す。
ここで, に
を代入すると,
なので,両辺 倍して から まで足し合わせると,
上記の入試問題の背景
上記の入試問題の背景
余談ですが,上記の入試問題の背景には「確率分布の間の距離」があります。以下は理解する必要はありませんが, 多くの入試問題の背景には高度な数学が潜んでいると意識しておくとよいでしょう。
※確率分布の距離
正の実数 が足して1を満たすとき確率分布とみなせます。そして 確率分布 と の距離(っぽいもの)を
で定義することが多いです。
(「確率分布同士の距離」がなぜこのように定義されるのか,そして定義して何が嬉しいのかは大学で学んでください)
「距離」が負になると直感に反してよろしくないので非負であって欲しいです。そして,実際に確率分布間の距離が非負であることが,さきほどの解答によって保証されます!
つまり,上記の入試問題は「確率分布間の距離は非負であることを示せ」と言い換えることができます。 対数和不等式の証明と応用もどうぞ。
三角関数も指数対数関数も,多項式で抑えてしまえば楽になることが多いです。











