ガウス記号の定義と３つの性質

• 例えば，$x=2.1$ のとき，$2\leq 2.1<3$ なので $n=2$，つまり $\lfloor 2.1\rfloor=2$ です。
• $x=-4.3$ のとき，$-5\leq -4.3<-4$ なので $\lfloor -4.3\rfloor=-5$ です。
• $\lfloor x\rfloor$ は $x$ を超えない最大の整数，と言うこともできます。

ただし，$x$ がマイナスの場合は注意が必要です。$-4.3$ の整数部分は $-4$ と言いたくなりますが，さきほど見たように $\lfloor -4.3\rfloor=-5$ です。 迷ったら「きちんとした定義」を使いましょう。

「切り捨て，整数部分」などの言葉が出てきたらガウス記号を連想しましょう。ただし，実際に問題を解くときはほとんどの場合「きちんとした定義」の不等式を使うことになります。

ガウス記号に対して苦手意識を持っている人は多いですが，ガウス記号にまつわる問題は丁寧な場合分け＆簡単な不等式処理で解けることが多いです。

• $\lfloor x\rfloor$ ではなく $[x]$ と書くこともあります。むしろ高校数学・大学入試では $[x]$ を用いることが多いです。

• この記事では，$\lfloor x\rfloor$ と $[x]$ の両方をガウス記号と呼んでいますが，一般的に「ガウス記号」と呼ばれるのは $[x]$ のみのようです。

• ガウス記号（切り捨て）は $\lfloor x\rfloor$ ですが，逆に切り上げを $\lceil x\rceil$ と書くことがあります。天井関数などと呼びます。切り上げと切り捨てをセットにすると覚えやすいので，$[x]$ よりも $\lfloor x\rfloor$ と書く方がわかりやすいです。

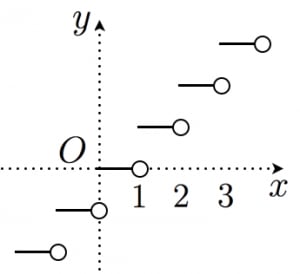
ガウス記号に慣れるために $y=\lfloor x\rfloor$ のグラフを描いてみます。

• $0\leq x <1$ のとき $y=0$
• $1\leq x <2$ のとき $y=1$
• $-1\leq x <0$ のとき $y=-1$

などに注意すると，$y=\lfloor x\rfloor$ のグラフは図のようになります。

同様に，$y=\lfloor x\rfloor+\lfloor 2x\rfloor+3x$ などのもっと複雑な関数のグラフも，場合分けがめんどうになりますが，丁寧に場合分けすればかくことができます。

ガウス記号には様々な性質がありますが，特に以下の3つは覚えておくとよいでしょう。

性質1は「$x+N$ の整数部分は $x$ の整数部分に $N$ を足したもの」という意味であり，明らかです。$y=\lfloor x\rfloor$ のグラフからも分かります。

性質2も「二つの数を足してから切り下げたもの」は「二つの数を切り下げてから足したもの」以上であるというのは明らかです。性質2のエレガントな応用例として，連続するn個の整数の積と二項係数があります。

性質3は後できちんと証明します。

$\lfloor 2x\rfloor=\lfloor x\rfloor+\left\lfloor x+\dfrac{1}{2}\right\rfloor$ を証明します。ガウス記号の問題は丁寧に場合分けするのみです。

ちなみに，性質3は以下のように一般化できます：

性質3’： $\lfloor nx\rfloor=\displaystyle\sum_{k=0}^{n-1}\left\lfloor x+\dfrac{k}{n}\right\rfloor$

（$n$ は任意の整数）

これを，エルミートの恒等式（Hermite’s identity）と言います。

→高校数学の問題集　～最短で得点力を上げるために～のT134では，ガウス記号に関する問題と2通りの解答を紹介しています。