決定係数の定義と相関係数との関係
決定係数 とは,予測式の精度(予測式によってデータをどれくらい説明できているか)を表す値です。
回帰分析の重要な概念である 決定係数 について詳しく解説します。 決定係数の意味 や,決定係数と相関係数の関係 について紹介します。
決定係数のイメージ
決定係数のイメージ
決定係数は,予測式(回帰式,回帰モデル)の精度を表す値です。
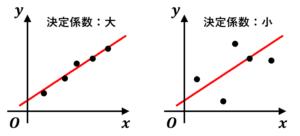
例えば,左側の図では,予測式がデータにうまく当てはまっているので決定係数が大きくなります(決定係数が に近くなります)。
右側の図では,予測式でデータをあまり説明できていないので,決定係数は小さくなります(決定係数が に近くなります)。
決定係数は という記号で表されることが多いです。
決定係数の定義
決定係数の定義
決定係数 の定義はいくつかありますが,以下の式で定義することが多いです:
ただし, たちがデータ, は の平均, は予測式を表します。
第二項の分母は全変動と呼ばれ,データのそもそものばらつき具合を表します。分子は残差変動と呼ばれ,回帰モデルと実測値とのズレを表します。
決定係数が に近い
残差変動が(全変動に比べて)小さい
よい予測式である
とみなせます。
決定係数はマイナスになるか
決定係数はマイナスになるか
決定係数のことを と書いていますが,これは必ずしも何かの二乗になるという意味ではありません。
あまりにひどいモデルを考えると,決定係数をマイナスにすることもできます。
しかし,単純に という定数関数(テキトーなモデル)を考えると決定係数は となります。つまり,決定係数がマイナスであるようなモデルはこのテキトーな定数関数にも負けるモデルということになり,考える意味はなさそうです。
決定係数=相関係数の二乗
決定係数=相関係数の二乗
最小二乗法による直線フィッティングの場合,相関係数の二乗と決定係数は一致する。
つまり「もともとのデータの相関係数の絶対値が大きいほど最小二乗法による直線フィッティングの精度がよくなる」と言えます。
相関係数と決定係数は全く別の文脈で(それぞれが意味を持つように)定義された量なので,その両者の間に美しい関係があるというのは驚きです!
また,定理により(最小二乗法による直線フィッティングの場合は)決定係数が 以上 以下の値を取ることも分かります。
※相関係数が 以上 以下になることの証明は,シュワルツの不等式を使ってできます:
定理の証明
定理の証明
定理の証明には以下の前提知識が必要となります。
-
最小二乗法による最適な直線 において , が成立する。 →最小二乗法(直線)の簡単な説明
-
「全変動ー残差変動=回帰変動」 →全変動,回帰変動,残差変動の意味と関係
決定係数を変形していく。全変動ー残差変動=回帰変動なので,
である。あとは比較的単純な式変形だけでできる。
これは相関係数の二乗に等しい!
決定係数を変形していって相関係数に一致したときの感動を多くの人に味わって欲しいです。
Tag:数学的モデリングまとめ(回帰分析)











