加法定理の証明のうち,余弦定理を用いる方法を紹介します。
加法定理の証明で一番有名な方法です。
証明の方針
step1. まず余弦定理を使って一般角に対して4(cosマイナス)を証明する
step2. 4を使って残りの5つを証明する
cosマイナスの証明
余弦定理を用います。加法定理の証明の核心部分です。
証明
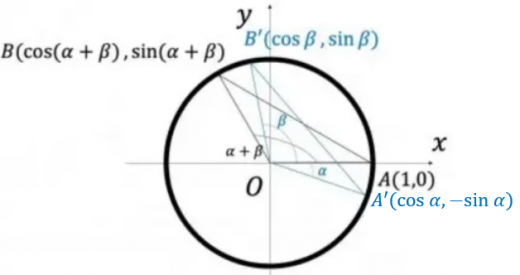
A(cosα,sinα),B(cosβ,sinβ)
とおくと
AB2=(cosα−cosβ)2+(sinα−sinβ)2=2−2cosαcosβ−2sinαsinβ

一方,OA
と
OB
のなす角を
θ
とおくと,三角形
OAB
に余弦定理を用いて
AB2=12+12−2⋅1⋅1cosθ=2−2cosθ
ここで,
任意の α,β に対して cosθ=cos(α−β) が成立する(重要な注)ので上の二式を比較して
cos(α−β)=cosαcosβ+sinαsinβ
を得る。
重要な注:
角度 θ
は 0 以上 π 以下です。よって,α−β(を 2π
で割った余り)が π 以下ならその値が θ になります。つまり cosθ=cos(α−β) です。一方,α−β(を 2π
で割った余り)が π より大きい場合,θ の「反対側の角度」に対応するので cosθ=cos{2π−(α−β)} です。後者の場合も後述の補助公式Bより cosθ=cos(α−β) となります。
残り5つの証明
一般角に対してcosマイナスが証明できてしまえば,あとは難しい発想は必要ありません。
補助公式
A.
sin(−θ)=−sinθ
,B.
cos(−θ)=cosθ
C.
sin(θ±2π)=±cosθ
,D.
cos(θ±2π)=∓sinθ
補助公式はとりあえず認めて下さい!(最後に補足します)
3(cosプラス)の証明
これはcosマイナスで β→−β とするだけです:
cos(α−(−β))=cosαcos(−β)+sinαsin(−β)
ここで,補助公式A,Bを使うと3を得ることができます。
2(sinマイナス)の証明
cosマイナスで位相をズラします:
例えば,β→β+2π
とします。
cos(α−(β+2π))=cosαcos(β+2π)+sinαsin(β+2π)
ここで,補助公式C,Dを使うと
sin(α−β)=sinαcosβ−cosαsinβ
となり3を得ることができます。
1(sinプラス)の証明
これはsinマイナスで β→−β とするだけです:
sin(α−(−β))=sinαcos(−β)−cosαsin(−β)
となり補助公式A,Bを使うと2を得ることができます。
5(tanプラス)の証明
1と3を使えばOKです:
tan(α+β)=cos(α+β)sin(α+β)=cosαcosβ−sinαsinβsinαcosβ+cosαsinβ=1−tanαtanβtanα+tanβ
ただし,最後の行は分母分子を
cosαcosβ
で割りました。
6(tanマイナス)の証明
2と4を使います。5と全く同様にできます。
補助公式について
険しい道のりはまだ続きます。三角関数の定義から加法定理を
厳密に証明するには補助公式A〜Dも一般角に対して証明しなければいけません(東大の問題はここまで要求しているのか分かりませんが)。
-
AとBについては図を書けばすぐに分かります。つまり,x
軸に関する折り返しで
(x,y)→(x,−y)
となるので
cos(−θ)=cosθ,sin(−θ)=−sinθ
となります。
-
CとDをきちんと証明するのはめんどうです。
「2π
回転で
(x,y)→(−y,x)
になること」
「−2π
回転で
(x,y)→(y,−x)
になること」
を言えばOKです。
 これを厳密に証明するには
(x,y)
がどの象限にあるかで場合分けしてやる必要があります。きちんと書くのは本当にめんどくさい(教科書にも書いていないレベル)ので図と図の説明を添えれば十分でしょう。
これを厳密に証明するには
(x,y)
がどの象限にあるかで場合分けしてやる必要があります。きちんと書くのは本当にめんどくさい(教科書にも書いていないレベル)ので図と図の説明を添えれば十分でしょう。
図の説明
- 青い点の一つを 2π 回転させると別の青い点へ移る
- 図の四つの直角三角形は相似&斜辺の長さが等しいので合同
よって,(x,y)
がどこにあっても
2π
回転で
(−y,x)
になり
−2π
回転で
(y,−x)
になることが確認できる。

 これを厳密に証明するには
がどの象限にあるかで場合分けしてやる必要があります。きちんと書くのは本当にめんどくさい(教科書にも書いていないレベル)ので図と図の説明を添えれば十分でしょう。
これを厳密に証明するには
がどの象限にあるかで場合分けしてやる必要があります。きちんと書くのは本当にめんどくさい(教科書にも書いていないレベル)ので図と図の説明を添えれば十分でしょう。