二次関数の軸と頂点の求め方など
-
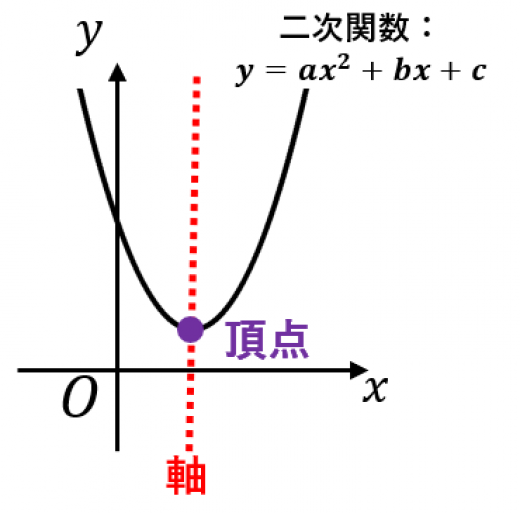
二次関数のグラフは, 軸と平行な「とある直線」に関して対称になる。この「とある直線」のことを二次関数の軸と言う。
-
また,二次関数のグラフと軸の交点のことを二次関数の頂点と言う。
二次関数の軸と頂点について,意味・公式とその導出・例題を整理しました。
軸と頂点の求め方
軸と頂点の求め方
二次関数 を平方完成して という形にすれば,軸と頂点がわかります。具体的には,軸は で頂点は になります。
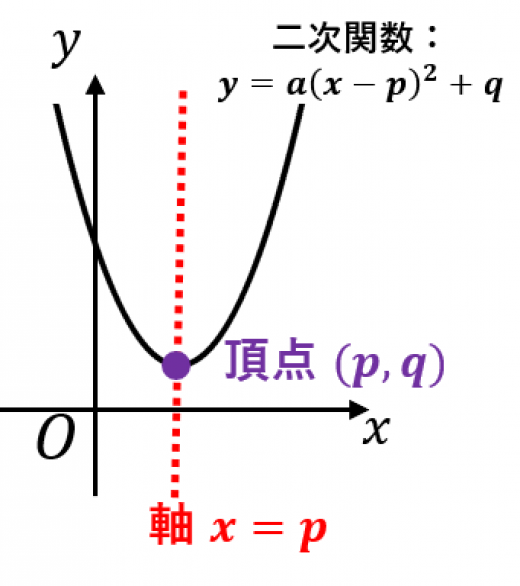
二次関数 の軸の方程式と頂点の座標を求めよ。
平方完成が不安な方は平方完成のやり方といくつかの発展形をどうぞ。
を平方完成する。
よって,
- 軸の方程式は
- 頂点の座標は
→高校数学の問題集 ~最短で得点力を上げるために~のT81では,この問題の3通りの解法と計算ミスを減らすコツを紹介しています。
二次関数の軸と頂点を求める公式
二次関数の軸と頂点を求める公式
さきほどの例題で見たように,平方完成すれば軸と頂点がわかります。一般の場合にやってみると以下の公式が得られます。
二次関数 において,
軸の方程式は
頂点の座標は
を平方完成する:
よって,軸の方程式は ,頂点の座標は
二次関数 の軸の方程式と頂点の座標を求めよ。
公式において, とすると,
- 軸の方程式は ,つまり
- 頂点の 座標は
公式を覚えるべきか
公式を覚えるべきか
- 毎回平方完成すればよいだけなので,軸の方程式や頂点の座標の公式は覚えなくても問題はありません(平方完成の修得は必須です)。
- ただし,二次関数の軸の方程式(頂点の 座標)が必要になる機会はとても多いため, は覚えてしまうことをオススメします。
- 頂点の 座標は(覚えなくても構いませんが)判別式を として と書けば覚えやすいです。
軸の方程式(頂点の 座標)の他の解釈
軸の方程式(頂点の 座標)の他の解釈
は平方完成すればすぐに導出できましたが,他の理解の方法もあります。
実数解を持つ場合にしか通用しない考え方だが,頂点の 座標は二次方程式 の解の平均である。この二次方程式の解の和は解と係数の関係より であるので,これを で割れば頂点の 座標が求まる。
二次関数において,接線の傾きが となる点が頂点なので,その 座標は の解として求まる。
より と分かる。
たとえ簡単であったとしても,高校数学の教科書に載っている公式は網羅したいです。










