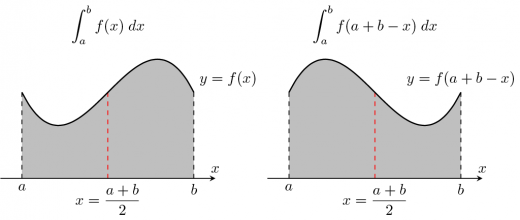
King Property は以下のテクニックと一緒に使われることが多いです。
テクニック
A=B のとき,A=2A+B
つまり,King Property と「テクニック」より
∫abf(x)dx=21∫ab{f(x)+f(a+b−x)}dx
となります。
三角関数の定積分
King Property の例として,
∫02πf(cosx)dx=∫02πf(sinx)dx
が成立します。sinのn乗,cosのn乗の積分公式でも紹介した式です。
この式を利用した,「不定積分を求めるのは難しいけど定積分なら求まる」ようなおもしろい例を紹介します。
問題1
I=∫02πsinx+cosxsinxdx
を求めよ。
解答
King Property より,I=∫02πsinx+cosxcosxdx
となる(y=2π−x
と置換すれば直接確認できる)。
よって,
I=21(I+I)=21(∫02πsinx+cosxsinxdx+∫02πsinx+cosxcosxdx)=21∫02π1dx=4π
ちなみに,この例では頑張れば不定積分を求めることもできます。→三角関数の有理式の積分
指数関数の定積分
問題2
I=∫−111+e−2xdx
を求めよ。
解答
分母分子に
ex
をかけると問題1のような形になる:
I=∫−11ex+e−xexdx
また,King Property より
I=∫−11ex+e−xe−xdx
(y=−x
と置換すると直接確認できる)
よって,
I=21(I+I)=21∫−111dx=1
→高校数学の問題集 ~最短で得点力を上げるために~のT24では,この問題の別解と計算ミスを減らすコツを紹介しています。
対数関数の定積分
問題3
I=∫04πlog(1+tanx)dx を求めよ。
解答
y=4π−x と置換すると,
I=∫4π0log{1+tan(4π−x)}(−1)dx=∫04πlog(1+1+tanx1−tanx)dx=∫04πlog1+tanx2dx=∫04π{log2−log(1+tanx)}dx=4πlog2−I
よって,I=8πlog2
入試問題
問題4(長崎大学2023)
I=∫12x2+(3−x)2x2dx を求めよ。
解答
y=3−x と置換すると,
I=∫21(3−y2)+y2(3−y)2(−dy)
よって,I+I=∫121ddx=1
I=21