各点収束と一様収束の違いと具体例

更新 2023/04/17

関数列の収束には各点収束と一様収束という2つの概念があり，一様収束の方が強い。大雑把な意味は，

各点収束 → 各点でそれぞれ収束
一様収束 →すべての点が一気に収束

「各点収束」と「一様収束」の意味と関係を解説します。

関数列の収束

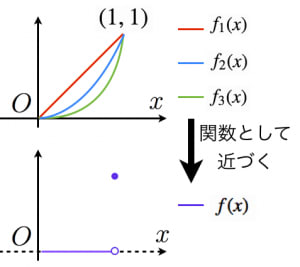
数列や関数の極限は高校数学で扱いますが，回は「関数列」の極限を考えます。関数が $f_1(x),f_2(x),\cdots$ のようにたくさんある状況をイメージしてください。

例

$f_n(x)=\dfrac{x}{n}\:(0\leq x\leq 1)$ という関数列の極限はどうなるか？

$f_1(x)=x$ ， $f_{2}(x)=\dfrac{x}{2}$ ， $f_{3}(x)=\dfrac{x}{3},\cdots$ というように $n$ が増えると $0$ という関数に近づいていきます。

一様収束の例

この「関数として近づく」というのを数学的に定義しようとしたときに，2種類の「収束」が登場します。

各点収束の定義と具体例

各点収束の定義

区間内の任意の点 $a$ に対して， $\displaystyle\lim_{n\to\infty}f_n(a)=f(a)$ が成立するとき，関数列 $f_n(x)$ は $f(x)$ に各点収束すると言う。

$x$ の値を $a$ に固定すれば， $f_1(a),f_2(a),\cdots$ は数列として扱えます。その数列が $f(a)$ に収束するのが各点収束です。まさに各点（について）収束という感じです。

例題1

$f_n(x)=x^n\:(0\leq x\leq 1)$ が

$f(x) = \begin{cases} 0 & (0 \leq x < 1) \\ 1 & (x=1) \end{cases}$

に各点収束することを確認せよ。

各点収束する例

解答

$x=a$ と固定して数列 $f_n(a)$ を考えると，

$0\leq a < 1$ のとき $\displaystyle\lim_{n\to\infty}f_n(a)=0$ ，
$a=1$ のとき $\displaystyle\lim_{n\to\infty}f_n(a)=1$

となるので $f_n(x)$ は $f(x)$ に各点収束する。

一様収束の定義と具体例

一様収束の定義

$\displaystyle\lim_{n\to\infty}\sup_x |f_n(x)-f(x)|=0$ のとき，関数列 $f_n(x)$ は $f(x)$ に一様収束すると言う。

全体が一様に（一気に）収束するというイメージです。

$\displaystyle\sup_x|f_n(x)-f(x)|$ は， $f_n(x)$ と $f(x)$ がどれくらい離れているかを「一番離れているところで測った値」です。sup の意味は sup（上限）とinfの意味，maxとの違いを参照してください。

例題2

さきほどの例題において $f_n(x)=x^n\:(0\leq x\leq 1)$ が $f(x)$ に一様収束しないことを確認せよ。

解答

$\displaystyle\sup_x|f_n(x)-f(x)|$ が $0$ に収束しないことを証明すればよい。実際， $x=2^{-\frac{1}{n}}$ に対して $|f_n(x)-f(x)|=\dfrac{1}{2}$ となるので，任意の $n$ に対して $\displaystyle\sup_x|f_n(x)-f(x)|\geq \dfrac{1}{2}$ である。つまり，一様収束しない。

コメント： $x=1$ 付近のせいで， $f_n(x)$ が $f(x)$ に一気に近づくことはないというイメージです。

例題3

$0\leq x\leq 1$ において関数列 $f_n(x)=\dfrac{x}{n}$ が $f(x)=0$ に一様収束することを確認せよ。

解答

$|f_n(x)-f(x)|=\dfrac{x}{n}\leq \dfrac{1}{n}$ より， $f_n(x)$ と $f(x)$ の距離（一番離れている所）は $\dfrac{1}{n}$ である。よって， $\displaystyle\lim_{n\to\infty}\sup_x |f_n(x)-f(x)|=0$ となり一様収束することが分かる。

例題4（難しい）

$M$ を定数とする。 $0 < x < M$ において関数列 $f_n (x) = \left( 1-\dfrac{x}{n} \right)^n$ が $f(x) = e^{-x}$ に一様収束することを示せ。

※例題4の結果はガンマ関数（階乗の一般化）の定義と性質で使います。

例題4の解答

解答

$\log f_n (x)$ が $-x$ に一様収束することを示せばよい。

$\begin{aligned} \log f_n (x) &= \log \left( 1-\dfrac{x}{n} \right)^n\\ &= n \log \left( 1-\dfrac{x}{n} \right)\\ &= n \sum_{k=1}^{\infty} \dfrac{1}{k} (-1)^{k+1} \left( -\dfrac{x}{n} \right)^k\\ &= - n \sum_{k=1}^{\infty} \dfrac{1}{k} \left( \dfrac{x}{n} \right)^k\\ &= -x - x \sum_{k=2}^{\infty} \dfrac{1}{k} \left( \dfrac{x}{n} \right)^{k-1} \end{aligned}$ と変形される。

$\displaystyle S_n (x) = x \sum_{k=2}^{\infty} \dfrac{1}{k} \left( \dfrac{x}{n} \right)^{k-1}$ とおく。 $S_n$ が $0$ に一様収束することを示す。

正数 $\varepsilon$ を任意に取る。

$K$ を十分大きく取ることで $x \sum_{k=K}^{\infty} \dfrac{1}{k} \left( \dfrac{x}{n} \right)^{k-1} < \dfrac{1}{2} \varepsilon$ とできる。

一方 $N$ を十分大きく取ることで $n > N$ で $x \sum_{k=2}^{K-1} \dfrac{1}{k} \left( \dfrac{x}{n} \right)^{k-1} < \dfrac{1}{2} \varepsilon$ とできる。

こうして十分大きな $n$ に対して $S_n (x) < \varepsilon$ とできる。

以上より $S_n (x)$ は $0$ に一様収束する。

つまり $f_n$ は $e^{-x}$ に一様収束する。

一様収束は各点収束より強い

一様収束と各点収束の関係

一様収束すれば各点収束する
各点収束しても一様収束するとは限らない

1つめは，関数として一気に近づけば当然各点で見ても近づいていくことから理解できるでしょう。

2つめについては例題1，2の関数が例になっています。

一様収束の嬉しさ

一様収束が嬉しいのは以下の定理が成り立つからです！

定理

連続関数列の一様収束極限は連続関数

連続関数列の収束先が連続でないと悲しいです（例えば例題1）が，一様収束という強い意味で収束してくれれば，収束先も連続なのでハッピーという主張です。

注：「一様収束」は「一様連続」と混同しやすいので注意して下さい。→関数の連続性と一様連続性

また，一様収束だと積分と極限（シグマ）が交換できるので嬉しかったりもします。→積分と極限（無限和）の交換

無限級数との関連

定理

$\displaystyle f(x) = \sum_{n=0}^{\infty} a_n (x-a)^n$ とする。収束半径を $r$ とする。

このとき $\displaystyle f_N (x) = \sum_{n=0}^{N} a_n (x-a)^n$ は $|x-a| < r$ で広義一様収束する。

なお，収束半径については収束半径の意味と求め方をどうぞ。

ゴールデンウィークだからといって外出する必要はありません。家でのんびり数学するのも一興。

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！