ヒストグラムとは&注意点
データを整理する代表的な手法の一つであるヒストグラム(柱状グラフ,頻度分布図)について解説します。
ヒストグラムとは
ヒストグラムとは
ヒストグラムとは,図のような柱状のグラフのことです。基本的には 横軸は階級,縦軸は度数(その階級に属するデータの数)を表します。
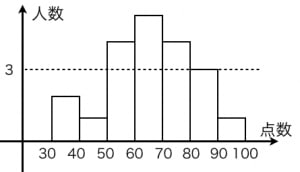
例えば, 人のテストの点数が
のとき,階級の幅を としたヒストグラムは図のようになります。
全員ぶんのテストの点数の一覧(情報量が多すぎる)を見るよりもヒストグラムを見たほうが全体の様子が分かりやすいですね。
※厳密には,高さではなく面積が度数に比例するような長方形を書きます(階級の幅が階級ごとに異なる場合にのみ注意が必要です)。
階級の幅
階級の幅
ヒストグラムを書く際には階級の幅を適切に定める必要があります。階級の幅が広すぎると,多くのデータが同じ階級としてカウントされてしまい,情報が落ちてしまいます。一方,階級の幅が狭すぎると1つのデータも属さないような階級が多くなり,分布の様子がよく分かりません。
階級の幅の決め方については,いくつか経験的な公式のようなものがありますが「この公式に従えば絶対よい」というような決定版はありません。そのため,簡単なデータの分析ではいくつかやってみて一番分布の様子が分かりやすい幅(主観的になってしまいますが)を採用するのが現実的です。
ヒストグラムの重要性
ヒストグラムの重要性
「データの平均や分散を求めよ」という問題は多いですが「データのヒストグラムを書け」という問題はほとんど見かけません(出題しにくい)。そのため,実際のデータが与えられたときに平均や分散を求めて満足しがちですが,平均や分散などは分布の一つの特徴量にすぎず,かなり情報が少ないです。
一方,ヒストグラムを使えば分布の全体的な様子を見ることができるので効果的です。そのため,実際にデータの全体的な様子を把握したいときは,平均や分散などの特徴量のみから考えるのではなく,ヒストグラム(または度数分布表)を使うのがおすすめです。
ヒストグラムは高校数学の教科書(数学1)で少しだけ登場します。











