変曲点の意味といろいろな例
変曲点について,定義・意味・求め方をわかりやすく解説します。
後半では,具体例(三次関数,四次関数,正規分布)を通じて変曲点の理解を深めます。
変曲点の定義
変曲点の定義
-
変曲点とは,「上に凸」と「下に凸」がきりかわる点のことです。
-
変曲点は「二階微分の符号が変化する点」と言うこともできます。
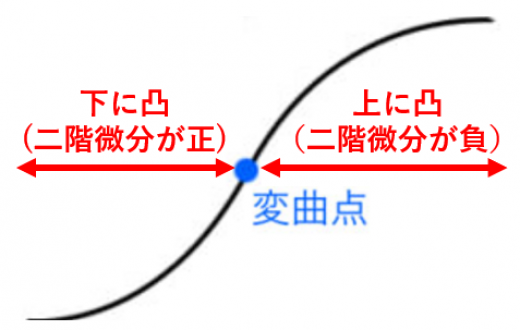
※二階微分と「上に凸」「下に凸」の関係は →上に凸,下に凸な関数と二階微分で解説しています。
変曲点の意味
変曲点の意味
変曲点には「グラフの曲がり方が変わる点」という意味がある。
文字通り「変曲点」というわけです。
変曲点は「二階微分の符号が変化する点」であった。
「二階微分の符号がプラスからマイナスに変化する」ということは,「一階微分が増加から減少にきりかわる」ということ。
つまり,「接線の傾きが増加から減少にきりかわる」ということ。
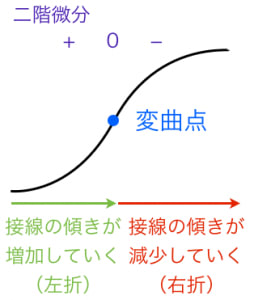
これは「曲がり方が変わる(ハンドルの切り方が変わる)」と解釈できる。二階微分がマイナスからプラスに変化する場合も同様。
変曲点の求め方
変曲点の求め方
変曲点において,二階微分
つまり,変曲点を求めるためには,二階微分 を計算して を解けばよいわけです。
の変曲点を計算してみる。
微分は
二階微分は,
よって, を解くと であり, の前後で の符号がマイナスからプラスにきりかわる。このとき 座標は よって,変曲点の座標は
重要な注意
「変曲点ならば二階微分 」は成立しますが,その逆「 ならば変曲点」は成立しません。二階微分が0でも符号が変化する点とは限らないからです。
の変曲点を計算してみる。 なので, の解は 。ただし, はずっと非負であり, の前後で符号がマイナスに変化することはない。よって,変曲点は無い。
つまり,変曲点の求め方は,以下のようになります(手順2が必要です)。
手順1. を解いて変曲点の候補を見つける。
手順2. 実際に の符号が変化するかどうかを確認する。
三次関数の変曲点
三次関数の変曲点
三次関数の変曲点は,必ずただ一つ存在する。
任意の三次関数は と書ける。
よって, で二階微分の符号が変化するので変曲点である。
実は,三次関数の変曲点について,追加で以下の2つの定理が成立します。
- 三次関数は変曲点に関して点対称である。
- 変曲点に関連して「四等分の法則」が成立する。
「四等分の法則」の意味と,上記2つの定理の証明は →三次関数の対称性と4等分の法則
四次関数の変曲点
四次関数の変曲点
四次関数の変曲点は0個または2個。
二階微分が二次関数となるので,二階微分の符号変化点の数は0個または2個になる。
- 変曲点が0個の例:
- 変曲点が2個の例: →四次関数のグラフの概形と例題2問
正規分布の変曲点
正規分布の変曲点
続いて, という関数の変曲点について考えます。この関数は,正規分布の確率密度関数という意味でとても重要です。
の変曲点を求めよ。
よって, が変曲点の 座標。変曲点の 座標は
特に, とすると, の変曲点は であることが分かります。
さらに,平行移動と拡大を用いることにより, 正規分布の確率密度関数: の変曲点は であることが分かります。
つまり,以下が証明できました。
正規分布において,変曲点の 座標は,1シグマ区間の端っこ(平均 標準偏差)
人生山あり谷あり変曲点あり。











