ハノイの塔のルールと最短手数

更新 2021/03/07

$n$ 段のハノイの塔の最短手数は $2^n-1$

「ハノイの塔」というゲームのルールと解き方を紹介します。

ハノイの塔のルール

3本の柱がある。そのうちの1本に
nnn
 段の塔がある（下段ほど大きい，図は
n=3n=3n=3
 の場合）。
目標：nnn
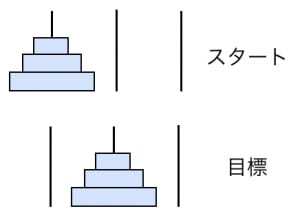
段の塔を別の柱に移したい。
できること：「ある柱の一番上の段を別の柱（の一番上）に移動させる」という操作を何度でもできる。
条件：途中で「小さい段の上に大きい段がある」という状況を作ってはいけない。
以上がハノイの塔のルールです。この記事ではハノイの塔の目標達成に必要な手数の最小値，および実際に最小値を達成する方法を考えてみます。

漸化式を立てる

$n$ 段の塔を移動させるのに必要な最小手数を $a_n$ とします。 $a_n$ についての漸化式を立てます。

漸化式の導出

「 $n$ 段を移動する」という作業は以下の3つの作業により達成できる。

$n-1$ 段を別の柱に移動する
最下段を（空いている柱が1本あるのでそこに）移動する
$n-1$ 段を最下段の上に移動する

逆に「 $n$ 段を移動する」ためにはこの3つの作業が絶対に必要である。

よって， $a_n=a_{n-1}+1+a_{n-1}$

つまり， $a_n=2a_{n-1}+1$

漸化式を解く

初期条件 $a_1=1$ を使ってさきほどの漸化式を解きます。

漸化式は

$a_n+1=2(a_{n-1}+1)$

と変形できるので，

$a_n+1$ という数列は，初項が $a_1+1=2$ ，公比が $2$ の等比数列である。

よって， $a_n+1=2^n$

したがって， $a_n=2^n-1$

最短手数を達成する方法

「漸化式の導出」から最短手数を達成する再帰的なアルゴリズムを構成できます。

$n$ 段のハノイの塔に対するアルゴリズム $A(n)$

$n=1$ なら1段目を移動するだけ
$n\geq 2$ なら $A(n-1)$ を用いて $n-1$ 段を移動する $n$ 段目（最下段）を移動する $A(n-1)$ を用いて $n-1$ 段を $n$ 段目の上に移動する

高校数学で習う漸化式が役立つ身近な例です。

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！