アダマール行列の定義と性質
更新
各要素が または で,各行が互いに直交するような正方行列をアダマール行列 (Hadamard matrix) と言う。
アダマール行列の例
アダマール行列の例
サイズ1の例: ,
サイズ2の例: ,
サイズ4の例:
はアダマール行列です。
がアダマール行列のとき, もアダマール行列になります。
アダマール行列の性質
アダマール行列の性質
が アダマール行列のとき,
性質1:
性質2: の各列も直交する
性質3: のサイズは ,または ,または の倍数
アダマール行列の定義より, ( は単位行列)
よって, の逆行列は となる。
よって,
これは の各列が互いに直交することを示している。
アダマール行列のサイズ
アダマール行列のサイズ
サイズ3以上のアダマール行列のサイズが の倍数になることを証明します。
のある列を 倍しても行ベクトルの直交性には影響を与えない。よって, の各列について適切に 倍することで,一行目が全て であるアダマール行列 を作ることができる。
また,列を交換しても行ベクトルの直交性には影響を与えないので,2行目が のものを左に集める。さらに,その中でも 行目が のものを左に集める。
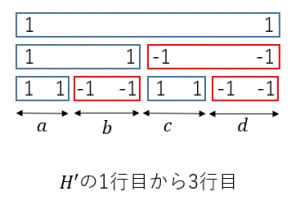
4つのブロックのサイズを とおく。
1行目と2行目の直交性から
1行目と3行目の直交性から
2行目と3行目の直交性から
以上から となる。
よって, のサイズが の倍数なので のサイズも の倍数である。
参考文献:Peter J. Cameron, Hadamard and conference matrices
ちなみに,全ての4の倍数サイズのアダマール行列が存在するかどうかは未解決問題らしいです。
自分にはこの記事に書いた程度の知識しかありませんが,実はかなり奥が深い行列のようです。











